Solved 4 C N 1 K A C N 1 K 1 C N 1 K 1 Chegg

Solved A в N 1в ћ 1 N 1n23n2 2n 4 C в N 0 1 N6n4n B в N 1в ћ Chegg Here is perhaps a simple proof the lhs i.e. $c (n, k)$ is the number of ways to select $k$ objects from $n$ distinct ones. now let us say we have marked a specific object and want to count the selections with and without this object. This video provides an algebraic proof for a binomial identity.
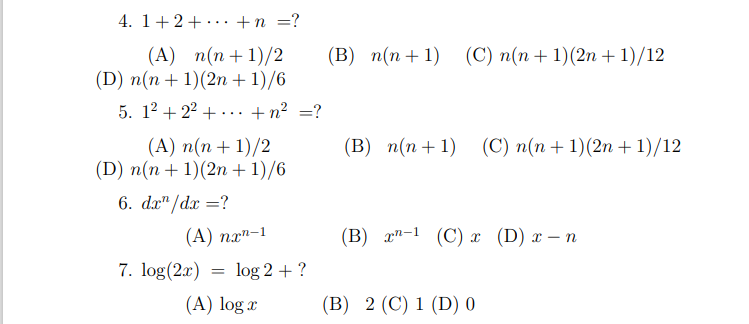
Solved 4 1 2 站ッ N A N N 1 2 B N N 1 C Chegg Our expert help has broken down your problem into an easy to learn solution you can count on. question: consider the identity kc (n, k) = nc (n 1, k 1), where 1 lessthanorequalto k lessthanorequalto n. (a) verify the identity for n = 10, k = 5. (b) give an algebraic proof of the identity. Find the number of ways of choosing r unordered outcomes from n possibilities as ncr (or nck). combinations calculator or binomial coefficient calcator and combinations formula. free online combinations calculator. A better approach would be to explain what \ ( {n \choose k}\) means and then say why that is also what \ ( {n 1 \choose k 1} {n 1 \choose k}\) means. let's see how this works for the four identities we observed above. This particular problem can be solved using a much simpler method, that does not use substitution. we can safely assume t (0) = k t (0) = k, where k k is positive constant, as for input size zero we need to do only a constant amount of work, e.g. checking input size and returning.

Solved 4 1 2 站ッ N A N N 1 2 B N N 1 C Chegg A better approach would be to explain what \ ( {n \choose k}\) means and then say why that is also what \ ( {n 1 \choose k 1} {n 1 \choose k}\) means. let's see how this works for the four identities we observed above. This particular problem can be solved using a much simpler method, that does not use substitution. we can safely assume t (0) = k t (0) = k, where k k is positive constant, as for input size zero we need to do only a constant amount of work, e.g. checking input size and returning. The number c (n,k) or `c " (n,k)"` is the the probability of choosing one specific set of elements from a set of n objects. the formula for the number of combinations is as follows:. Write your answers to the questions in parts ii, iii, and iv directly in this booklet. all work should be written in pen, except for graphs and drawings, which should be done in pencil. Developing techniques for answering these three questions will enable us to solve more open problems. let us explain it by some examples in the following. Your solution’s ready to go! enhanced with ai, our expert help has broken down your problem into an easy to learn solution you can count on. here’s the best way to solve it. not the question you’re looking for? post any question and get expert help quickly.
Comments are closed.