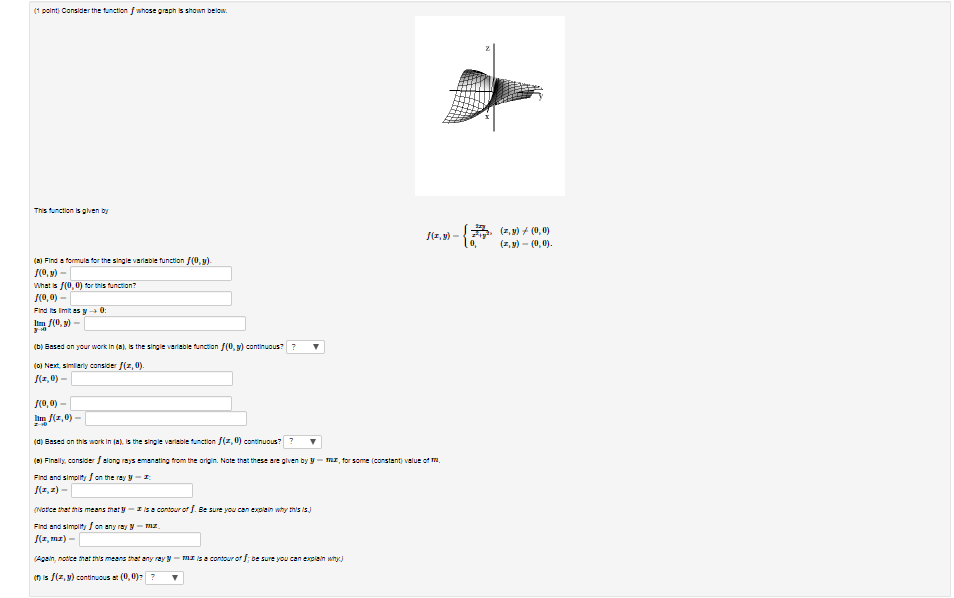
Solved 1 Point Consider The Function F Whose Graph Is Chegg Determine an upper estimate for the area under the curve f (x) = sin z between x = and x = π·show how you arrive at this estimate 3. determine a lower estimate for the area under the curve f (x) sin z between z and z π . Use the following graph of f (x) to determine the following items. if any limit is [infinity] or − [infinity] you must say so explicitly rather than writing "does not exist" or "dne".
Solved Consider The Function F Whose Graph Is Shown Below Chegg Question a. consider the function f (x) whose graph is shown below. based on the graph, fill in the table with the appropriate values. Q 1.find the local maximum and minimum values and saddle point (s) of the function. if you have three dimensional graphing. To calculate f′(1), we need to find the derivative of the function at x=1. from the graph, we can see that the slope of the curve at x=1 is positive and relatively steep, so the value of f′(1) is likely to be positive. If we look at 4 to 8 now, we're just looking from here over to here. it's still a big positive number, but it's missing a little bit of it, so it's not quite as big as see, so let's call it not as big.
Solved 1 Pt Consider The Function F Whose Graph Is Shown Chegg To calculate f′(1), we need to find the derivative of the function at x=1. from the graph, we can see that the slope of the curve at x=1 is positive and relatively steep, so the value of f′(1) is likely to be positive. If we look at 4 to 8 now, we're just looking from here over to here. it's still a big positive number, but it's missing a little bit of it, so it's not quite as big as see, so let's call it not as big. This problem has been solved! you'll get a detailed solution from a subject matter expert that helps you learn core concepts. To compare the integrals, we need to evaluate each of them based on the given intervals on the graph of the function f. we will analyze the signs (positive or negative) of the areas under the curve for each interval. For the function f whose graph is shown, list the following quantities in increasing order, from smallest to largest, and explain your reasoning. All answers are correct, assuming that the vertical axis has the same scale as horizontal, i.e., the grid lines are $1$ unit apart. it would be better if whoever made the graph placed some numbers on the vertical axis too.
Comments are closed.