Solved 1 Determine C Such That The System Has No Solutions Chegg
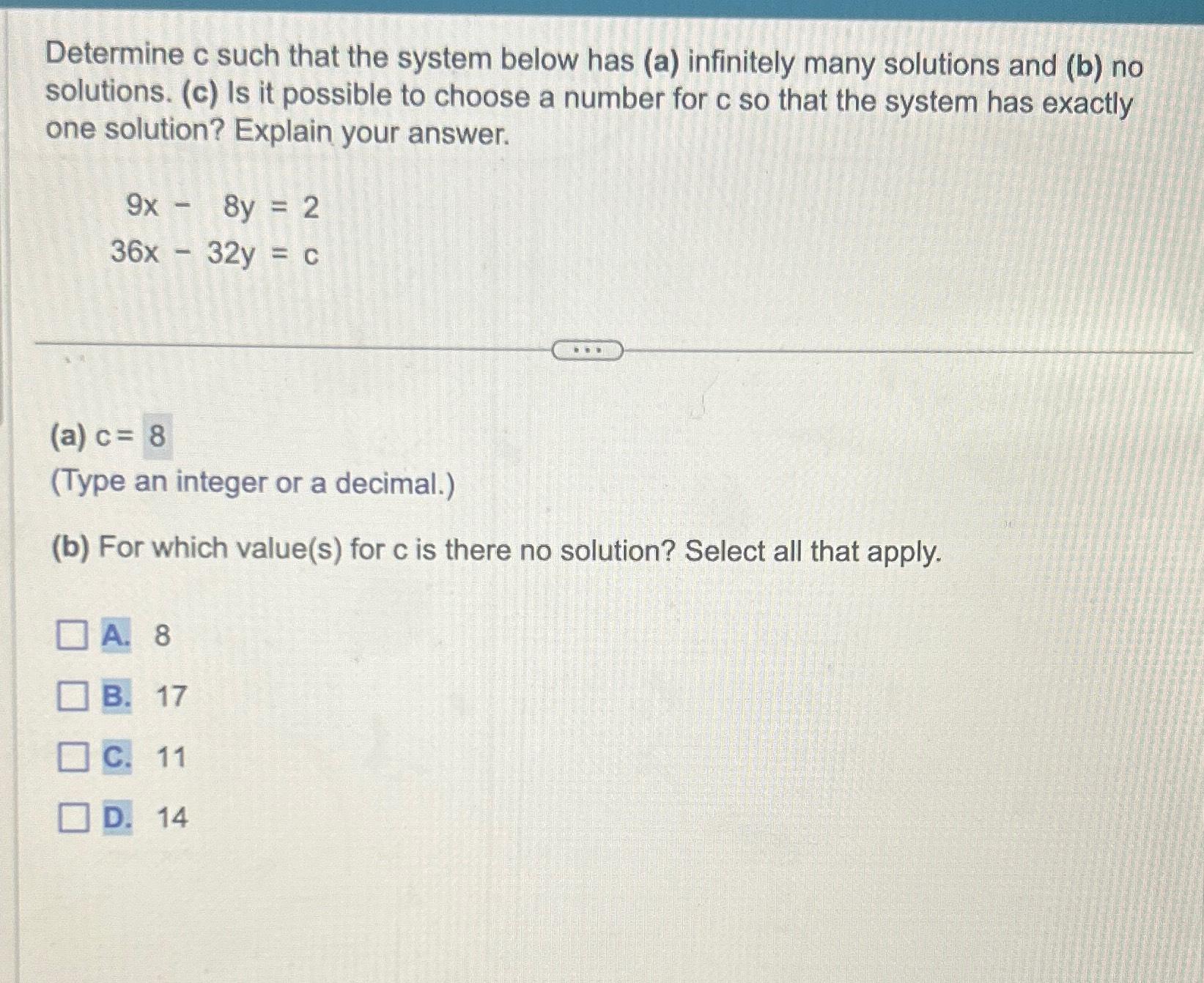
Solved Determine C ï Such That The System Below Has A Chegg Your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. see answer question: 1. determine c such that the system has no solutions. 9x−8y=227x−24y=c 2. determine c such that the system below has infinitely many solutions. 8x 5y=324x 15y=c 3. After mulling this over for a bit, i don't think there is a case where we have infinitely many solutions actually. that would mean i could write one row as a multiple of another row, but that's impossible for any choice of a a.
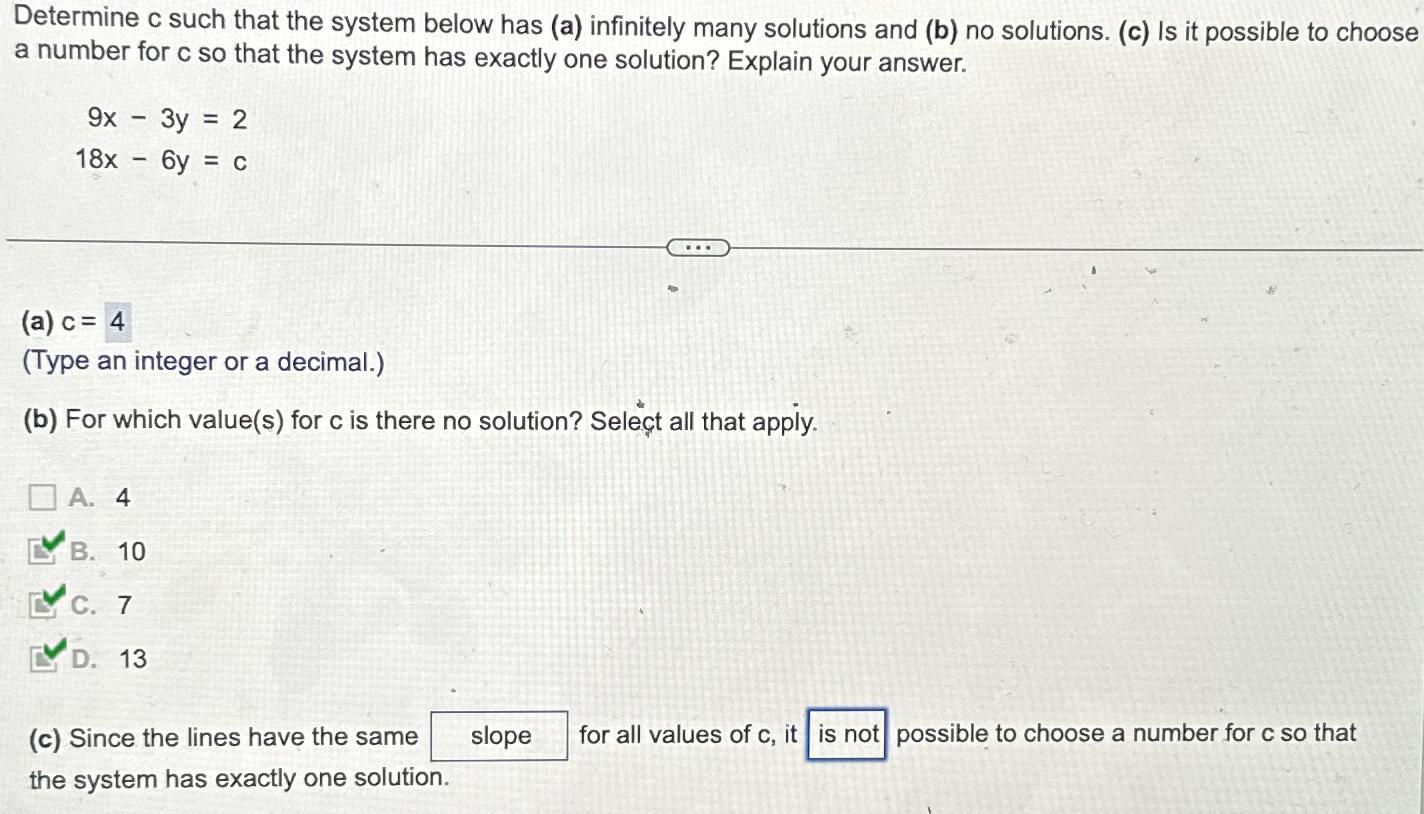
Solved Determine C ï Such That The System Below Has A Chegg 1. if c ≠ 6, then the system has no solutions 2. if c = 9, then the system has infinitely many solutions. 3. x ≈ 1.2614 y ≈ 3.5217 z ≈ 3.3471 note: these are approximate values exact values cannot be determined. To determine the conditions on 𝒃 for the given system of linear equations to have no solution, one solution, or infinitely many solutions, we can use the concept of the determinant of the coefficient matrix. To analyze the system of equations and determine the values of a for which the system has no solutions, exactly one solution, or infinitely many solutions, we can consider the three equations given:. The easiest way to proceed on this one is to note that if there is no solution, the determinant of the coefficient matrix must be zero. so the determinant of 1 1 5 1 2 2 4 11 k must be zero. this determinant can be worked out by hand resulting in the equation 2k 8 55 40 22 k = 0.

Solved Determine C ï Such That The System Has No Chegg To analyze the system of equations and determine the values of a for which the system has no solutions, exactly one solution, or infinitely many solutions, we can consider the three equations given:. The easiest way to proceed on this one is to note that if there is no solution, the determinant of the coefficient matrix must be zero. so the determinant of 1 1 5 1 2 2 4 11 k must be zero. this determinant can be worked out by hand resulting in the equation 2k 8 55 40 22 k = 0. We want to determine the values of h and k such that the system has no solution, a unique solution, or many solutions. the two equations can be interpreted as lines in a two dimensional space. depending on how these lines relate to each other, we can have different types of solutions:. Gaussian elimination: the algorithm for reducing a matrix to the row echelon form. this algorithm consists a forward phase of row operations in which zeros are introduced below the leading 1 s. as there is no value satisfies both equations so the system can t have infinite number of solutions. Now that we have several methods for solving systems of equations, we can use the methods to identify inconsistent systems. recall that an inconsistent system consists of parallel lines that have the same slope but different y intercepts. An example of a system of equations with no solutions is when the lines represented by the equations are parallel. on the other hand, a system with infinitely many solutions would involve identical equations, meaning they represent the same line on a graph.

Solved 1 Chegg We want to determine the values of h and k such that the system has no solution, a unique solution, or many solutions. the two equations can be interpreted as lines in a two dimensional space. depending on how these lines relate to each other, we can have different types of solutions:. Gaussian elimination: the algorithm for reducing a matrix to the row echelon form. this algorithm consists a forward phase of row operations in which zeros are introduced below the leading 1 s. as there is no value satisfies both equations so the system can t have infinite number of solutions. Now that we have several methods for solving systems of equations, we can use the methods to identify inconsistent systems. recall that an inconsistent system consists of parallel lines that have the same slope but different y intercepts. An example of a system of equations with no solutions is when the lines represented by the equations are parallel. on the other hand, a system with infinitely many solutions would involve identical equations, meaning they represent the same line on a graph.
Comments are closed.