Solved 1 Consider The Traffic Problem Below Where Chegg

Solved 2 Consider The Following Traffic Flow Problem At Chegg Question: 1. consider the traffic problem below, where c1,c2,c3,c4, and c5 are variables representing the cars on those streets, the arrows represent the direction of the streets, and the constants represent the number of cars entering or leaving that street during this hour. Set up a system of equations that determines the number of cars that can must travel on each interior road to satisfy the inputs outputs to the system. solve the above system, including a discussion of how many solutions you have.

Solved 1 Consider The Traffic Problem Below Where Chegg Problem 1 assumes that traffic assignment is deterministic. in reality, traffic assignment (route choice) varies across decision making motorists on the road. Consider the problem of calculating the pattern of traffic flow for a community. the network in this case consists of a system of streets and nodes, or intersections, where the roads meet. each street will have a certain rate of flow, measured in vehicles per some time interval. Through a few row operations we can get to this matrix shown below note: i'm skipping showing the row operation steps because it simply takes too much space on a forum such as this; however, if you need me to go over that, then just let me know and i'll try to figure something out. Low values of phf illustrated that there is significant variation of traffic volume within the peak hour volume and higher values of phf means the traffic volume is approximately equal within peak hour period.
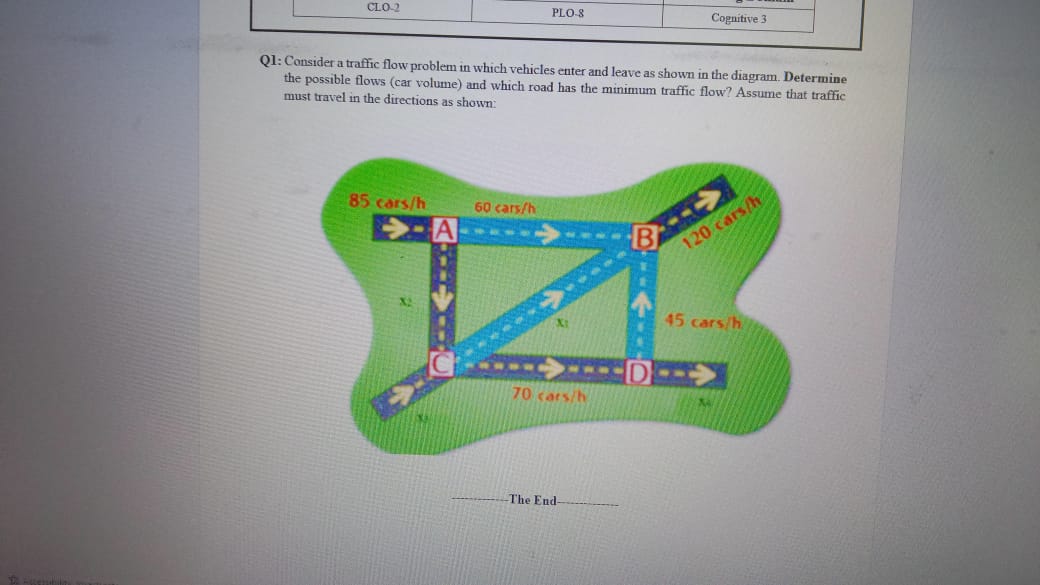
Solved Q1 Consider A Traffic Flow Problem In Which Vehicles Chegg Through a few row operations we can get to this matrix shown below note: i'm skipping showing the row operation steps because it simply takes too much space on a forum such as this; however, if you need me to go over that, then just let me know and i'll try to figure something out. Low values of phf illustrated that there is significant variation of traffic volume within the peak hour volume and higher values of phf means the traffic volume is approximately equal within peak hour period. To solve the system, we would typically use methods such as substitution or elimination. however, without specific equations derived from a detailed network diagram, we can't solve this step accurately. Consider the freeway and traffic conditions described in problem 6.3. if 180 of the 1800 vehicles observed in the peak hour were heavy vehicles (assume a 70% 30% sut tt split), what would the level of service of this freeway be on a 5 mi, 6% downgrade? here’s the best way to solve it. 1. consider the traffic deadlock depicted in the below figure. a. show that the four necessary conditions for deadlock indeed hold in this example. b. state a simple rule for avoiding deadlocks in this system. there are 3 steps to solve this one. To solve this problem, we need to use the poisson distribution formula, as the arrival rate of vehicles is given and the event of vehicles arriving can be considered as a poisson process.

Solved Consider The Following Traffic Problem Find The Chegg To solve the system, we would typically use methods such as substitution or elimination. however, without specific equations derived from a detailed network diagram, we can't solve this step accurately. Consider the freeway and traffic conditions described in problem 6.3. if 180 of the 1800 vehicles observed in the peak hour were heavy vehicles (assume a 70% 30% sut tt split), what would the level of service of this freeway be on a 5 mi, 6% downgrade? here’s the best way to solve it. 1. consider the traffic deadlock depicted in the below figure. a. show that the four necessary conditions for deadlock indeed hold in this example. b. state a simple rule for avoiding deadlocks in this system. there are 3 steps to solve this one. To solve this problem, we need to use the poisson distribution formula, as the arrival rate of vehicles is given and the event of vehicles arriving can be considered as a poisson process.
Comments are closed.