Solution Joint Marginal And Conditional Probabilities Studypool
Probability Marginal Conditional Joint Pdf In this section, we will learn more sophisticated methods of assigning probabilities. we will discuss how to calculate the probability of more complicated events from the probability of related events. As you can see in the equation, the conditional probability of a given b is equal to the joint probability of a and b divided by the marginal of b. let’s use our card example to illustrate. we know that the conditional probability of a four, given a red card equals 2 26 or 1 13.

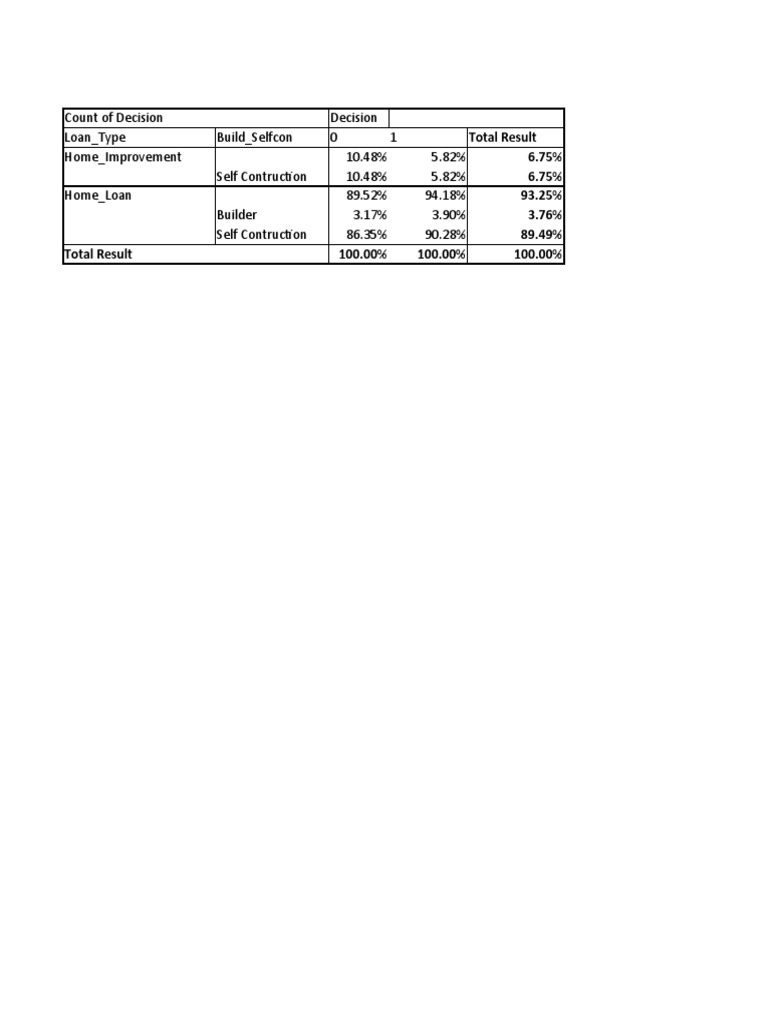
7 Joint Marginal And Conditional Distributions Pdf Covariance Study with quizlet and memorize flashcards containing terms like what is the sample space for a toss of a die? [6 2], the intersection of events a and b is [6 2a], joint probability of a and b and more. Joint probability is the probability of two or more events occurring simultaneously. marginal probability is the probability of an event irrespective of the outcome of other variables. conditional probability is the probability of one event occurring in the presence of one or more other events. We defined probabilities as the number of occurrences of an event divided by the total number of outcomes. this definition is fine as long as we know that we need to have many outcomes. In this section, we will explore marginal, joint, and conditional probabilities. we will do this using the data presented in the following two way table.

Solution Joint Marginal And Conditional Probabilities Studypool We defined probabilities as the number of occurrences of an event divided by the total number of outcomes. this definition is fine as long as we know that we need to have many outcomes. In this section, we will explore marginal, joint, and conditional probabilities. we will do this using the data presented in the following two way table. If there is no overlap between events, then the probability that one event or the other occurring is the sum of their individual probabilities. if two events do have overlap, given any two events 𝐴 and 𝐵, 𝑃 (𝐴 u 𝐵) = 𝑃 (𝐴) 𝑃 (𝐵) − 𝑃 (𝐴 ∩ 𝐵). Joint probability is the probability of two different events occurring at the same time. joint probability is calculated by taking the proportion of times that occurs divided by total number of frequencies. marginal probability is the probability of a single event irrespective of any other event. Understanding joint, marginal, and conditional distributions is crucial for data analysis and modeling: joint distributions capture the probability of multiple events occurring together. In this chapter we’ll be looking more at joint and marginal probabilities, i.e. considering the relationship between two separate events, starting with the assumption of independence, and then working to relax that assumption.

Solution Joint Marginal And Conditional Probabilities Studypool If there is no overlap between events, then the probability that one event or the other occurring is the sum of their individual probabilities. if two events do have overlap, given any two events 𝐴 and 𝐵, 𝑃 (𝐴 u 𝐵) = 𝑃 (𝐴) 𝑃 (𝐵) − 𝑃 (𝐴 ∩ 𝐵). Joint probability is the probability of two different events occurring at the same time. joint probability is calculated by taking the proportion of times that occurs divided by total number of frequencies. marginal probability is the probability of a single event irrespective of any other event. Understanding joint, marginal, and conditional distributions is crucial for data analysis and modeling: joint distributions capture the probability of multiple events occurring together. In this chapter we’ll be looking more at joint and marginal probabilities, i.e. considering the relationship between two separate events, starting with the assumption of independence, and then working to relax that assumption.

Solution Joint Marginal And Conditional Probabilities Studypool Understanding joint, marginal, and conditional distributions is crucial for data analysis and modeling: joint distributions capture the probability of multiple events occurring together. In this chapter we’ll be looking more at joint and marginal probabilities, i.e. considering the relationship between two separate events, starting with the assumption of independence, and then working to relax that assumption.
Comments are closed.