Solution Fourier Transform Example Studypool

10 Practice On Fourier Transform Pdf User generated content is uploaded by users for the purposes of learning and should be used following studypool's honor code & terms of service. Solution (a) the required fourier transform is the finite integral g (ω) = 1 √ 2 π ∫ − 1 sin ( 1 2 πx) e −iωx dx = −i 1 √ 2 π ∫ − 1 sin ( 1 2 πx) sin ωx dx, where only the sine survives because the rest of the integrand is odd. hence g (ω) = − 2 i 1 √ 2 π ∫ 1 0 sin ( 1 2 πx) sin ωx dx = − i √ 2 π ∫ 1 0 [.
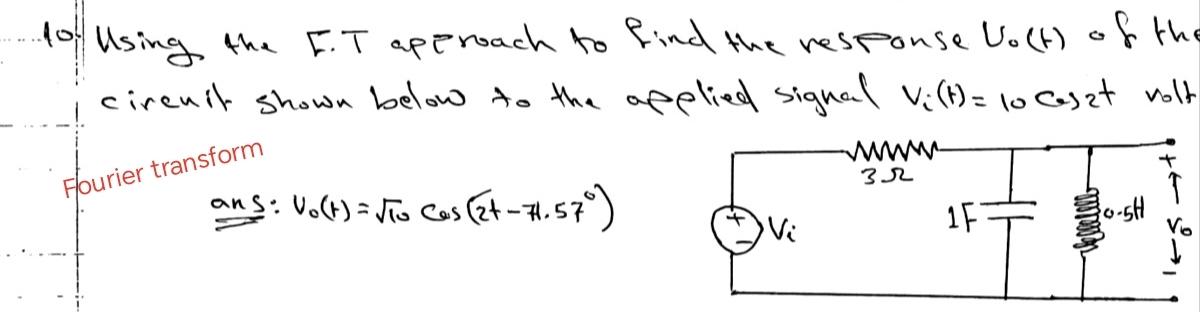
Solved I Need Solution For This Example In Fourier Transform Chegg Blems and solutions for fourier transforms and functions 1. prove the following results for fourier transforms, where f.t. represents the fourier transform, and f.t. [f(x)] = f (k): a) if f(x) is symmetr. c (or antisymme. ric), so is f (k): i.e. if f(x) = f. Abstract fourier transforms and laplace transforms have fundamental value to electrical engineers in solving many problems. waves are ubiquitous or found everywhere. perhaps the most basic wave is a harmonic or a sinusoidal wave. mathematical description of any type of wave was recognized early on, to be a combination of sinusoidal waves. To examine an example of am, we will assume that the signal from part (a) is multiplied by sin(2π50t). using sinesum2, plot the new signal, and explain how this can be done. Notes and video materials for engineering in electronics, communications and computer science subjects are added. "a blog to support electronics, electrical communication and computer students".

Solution Fourier Transform Studypool To examine an example of am, we will assume that the signal from part (a) is multiplied by sin(2π50t). using sinesum2, plot the new signal, and explain how this can be done. Notes and video materials for engineering in electronics, communications and computer science subjects are added. "a blog to support electronics, electrical communication and computer students". Fourier analysis is called a fourier transformation. its output, the fourier transform, is often given a more specific name, which depends on the domain and other properties. The fourier transform is the extension of this idea to non periodic functions by taking the limiting form of fourier series when the fundamental period is made very large (infinite). fourier transform finds its applications in astronomy, signal processing, linear time invariant (lti) systems etc. Solutions for practice problems for the final, part 3 note: practice problems for the final exam, part 1 and part 2 are the same as practice problems for midterm 1 and midterm 2. Example find the fourier series of the odd periodic extension of the function f (x) = 1 for x ∈ (−1, 0). solution: recall: 2 bn = nπ.

Solution Fourier Transform Studypool Fourier analysis is called a fourier transformation. its output, the fourier transform, is often given a more specific name, which depends on the domain and other properties. The fourier transform is the extension of this idea to non periodic functions by taking the limiting form of fourier series when the fundamental period is made very large (infinite). fourier transform finds its applications in astronomy, signal processing, linear time invariant (lti) systems etc. Solutions for practice problems for the final, part 3 note: practice problems for the final exam, part 1 and part 2 are the same as practice problems for midterm 1 and midterm 2. Example find the fourier series of the odd periodic extension of the function f (x) = 1 for x ∈ (−1, 0). solution: recall: 2 bn = nπ.

Solution Fourier Transform Studypool Solutions for practice problems for the final, part 3 note: practice problems for the final exam, part 1 and part 2 are the same as practice problems for midterm 1 and midterm 2. Example find the fourier series of the odd periodic extension of the function f (x) = 1 for x ∈ (−1, 0). solution: recall: 2 bn = nπ.

Solution Fourier Transform Full Notes Studypool
Comments are closed.