Solution Calculus 2 1 Tangent Lines And Velocity Class Notes Studypool

Solution Calculus 2 1 Tangent Lines And Velocity Class Notes Studypool Get help with homework questions from verified tutors 24 7 on demand. access 20 million homework answers, class notes, and study guides in our notebank. Problem 1: consider the function s ( t ) =− 12 ( t −1) 2 6 which models the trajectory of a ball thrown upward starting at time t = 0. let t be measured in seconds and s ( t ) in meters.

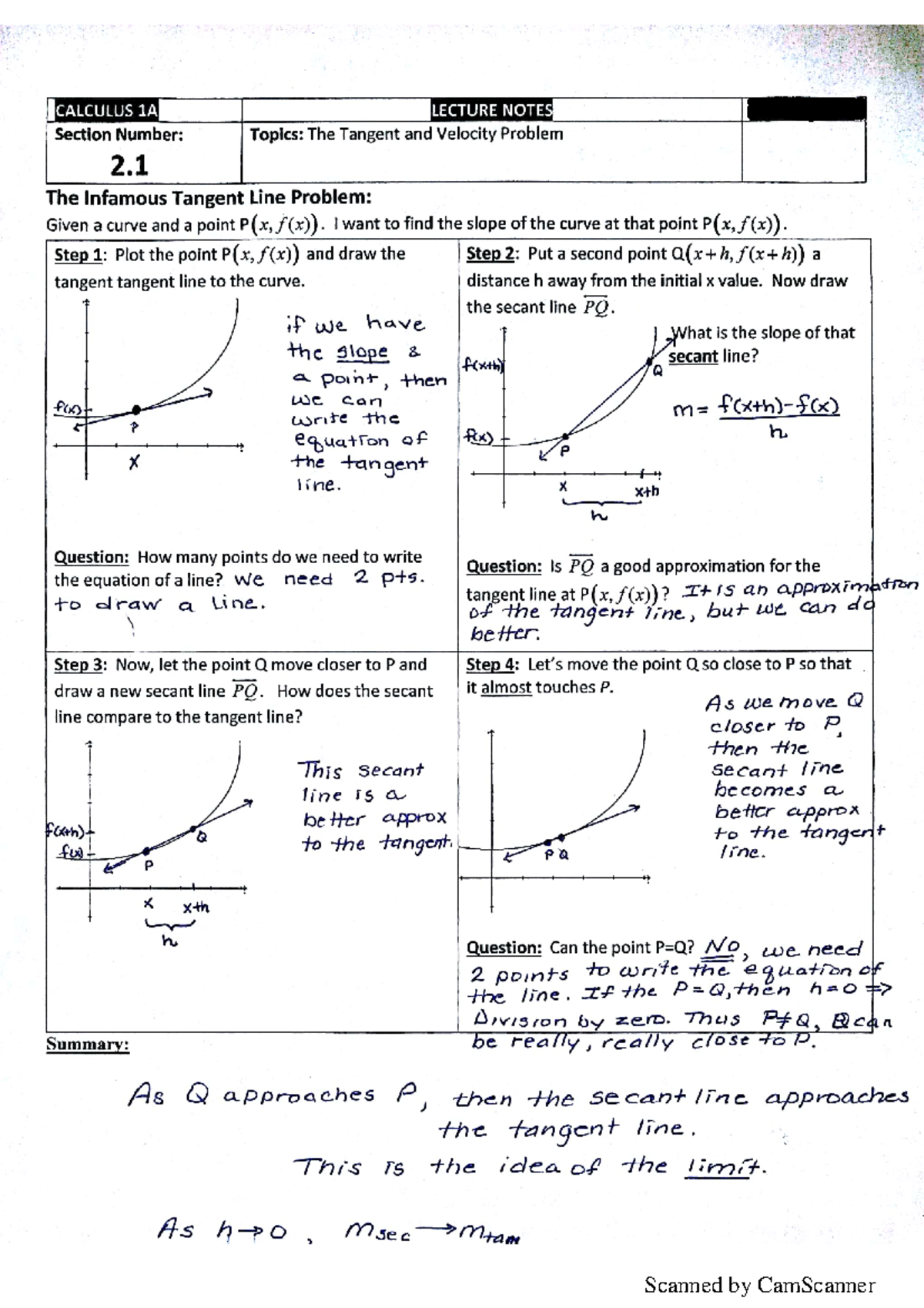
Lesson 2 1 The Tangent And Velocity Section Number 2 Lecture Notes It explains how to calculate average and instantaneous velocity, as well as the definitions of tangent and secant lines. additionally, it includes homework assignments related to the material covered in class. Calculus 140, section 2.1 tangent lines and velocity notes prepared by tim pilachowski we begin with the concept of limits in mathematics. non technically, taking a limit is moving constantly toward something without ever getting there. the first few homework exercises ask you to guess at the values of various limits. What is the slope of the secant line drawn to the right? what happens when h gets closer and closer to 0?. Preview text mat 281 blank notes unit 1 ­ 2 tangent and velocity problems 2 january 10, 2 tangent and velocity problems tangent line ­ a line that touches a curve and has the same direction at the point of tangency.

Calculus Notes The Tangent Line Problem Part 1 By Springboard Physics What is the slope of the secant line drawn to the right? what happens when h gets closer and closer to 0?. Preview text mat 281 blank notes unit 1 ­ 2 tangent and velocity problems 2 january 10, 2 tangent and velocity problems tangent line ­ a line that touches a curve and has the same direction at the point of tangency. Our solution involves finding the equation of a straight line, which is y − y0 = m(x − x0). we already know the tangent line should touch the curve, so it will pass through the point p(3, 1). In geometry, the tangent line (or simply tangent) to a plane curve at a given point is the straight line that "just touches" the curve at that point. leibniz defined it as the line through a pair of infinitely close points on the curve. The tangent problem: to find the equation of a tangent line to a curve at a specific point. the word tangent is derived from the latin word tangens, which means “touching”. Goals: de ne, compute, and draw secant and tangent lines. interpret the slope of secant and tangent lines.

Solution Calculus 1 Examination And Solution Studypool Our solution involves finding the equation of a straight line, which is y − y0 = m(x − x0). we already know the tangent line should touch the curve, so it will pass through the point p(3, 1). In geometry, the tangent line (or simply tangent) to a plane curve at a given point is the straight line that "just touches" the curve at that point. leibniz defined it as the line through a pair of infinitely close points on the curve. The tangent problem: to find the equation of a tangent line to a curve at a specific point. the word tangent is derived from the latin word tangens, which means “touching”. Goals: de ne, compute, and draw secant and tangent lines. interpret the slope of secant and tangent lines.

Solution Module 1 Calculus Notes Studypool The tangent problem: to find the equation of a tangent line to a curve at a specific point. the word tangent is derived from the latin word tangens, which means “touching”. Goals: de ne, compute, and draw secant and tangent lines. interpret the slope of secant and tangent lines.