Solution Applied Optimization Newtons Method Calculus With Solved

Calculus Optimization Problems Solutions Pdf Area Rectangle Here is a set of practice problems to accompany the newton's method section of the applications of derivatives chapter of the notes for paul dawkins calculus i course at lamar university. Typically, newton’s method is an efficient method for finding a particular root. in certain cases, newton’s method fails to work because the list of numbers \ (x 0,\, x 1,\, x 2,\, …\) does not approach a finite value or it approaches a value other than the root sought.
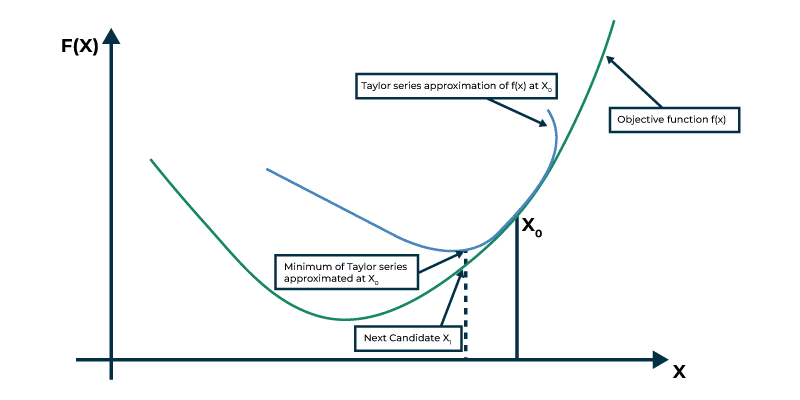
Optimization In Neural Networks And Newton S Method Geeksforgeeks Using a calculator (or a computer, if you wish), compute five iterations of newton’s method starting at each of the following points, and record your answers:. Absolute minimum. newton's method f (x) l (x) = f (x0) f0 (x0) (x x0) : extremely straightforward,. Newton's method uses curvature information (i.e. the second derivative) to take a more direct route. in calculus, newton's method (also called newton–raphson) is an iterative method for finding the roots of a differentiable function , which are solutions to the equation . Calculus i applications of derivatives 4.6. applied optimization 4.7. newton’s method 4.6. applied optimization solving applied optimization problems: 1. read the problem. 2. draw a picture and label parts that may be important to the problem. 3. introduce variables (or “unknowns”). find relationships between the unknowns. 4.

Calculus Optimization Math 126 Studocu Newton's method uses curvature information (i.e. the second derivative) to take a more direct route. in calculus, newton's method (also called newton–raphson) is an iterative method for finding the roots of a differentiable function , which are solutions to the equation . Calculus i applications of derivatives 4.6. applied optimization 4.7. newton’s method 4.6. applied optimization solving applied optimization problems: 1. read the problem. 2. draw a picture and label parts that may be important to the problem. 3. introduce variables (or “unknowns”). find relationships between the unknowns. 4. Thus at each iteration of the ||∇f(x)|| steepest descent method we step in the direction of −∇f(x) : x(k 1) ← x(k) − α∇f(x(k)) where α > 0 is a chosen step size, also known as the “learning rate” in some contexts. Explore newton's method for optimization, a powerful technique used in machine learning, engineering, and applied mathematics. learn about second order derivatives, hessian matrix, convergence, and its applications in optimization problems. In this question, you are asked to use newton’s method and the spreadsheet to find the optimal foraging time in problem 5.5 part (c) to 5 digits of accuracy. assume that k = 3 and a = 1 hrs, and t0 = 1 hrs, and use the energy gain function f (t) in problem 5.5. In this section we are going to look at a method for approximating solutions to equations. we all know that equations need to be solved on occasion and in fact we’ve solved quite a few equations ourselves to this point.

Solution Optimization Using Calculus Studypool Thus at each iteration of the ||∇f(x)|| steepest descent method we step in the direction of −∇f(x) : x(k 1) ← x(k) − α∇f(x(k)) where α > 0 is a chosen step size, also known as the “learning rate” in some contexts. Explore newton's method for optimization, a powerful technique used in machine learning, engineering, and applied mathematics. learn about second order derivatives, hessian matrix, convergence, and its applications in optimization problems. In this question, you are asked to use newton’s method and the spreadsheet to find the optimal foraging time in problem 5.5 part (c) to 5 digits of accuracy. assume that k = 3 and a = 1 hrs, and t0 = 1 hrs, and use the energy gain function f (t) in problem 5.5. In this section we are going to look at a method for approximating solutions to equations. we all know that equations need to be solved on occasion and in fact we’ve solved quite a few equations ourselves to this point.
Comments are closed.