Shooting Method For Boundary Value Problems Lecture 57 Numerical Methods For Engineers

Numerical Method For Engineers Chapter 8 Pdf Mathematical Analysis Shooting methods are developed to transform boundary value problems (bvps) for ordinary differential equations to an equivalent initial value problem (ivp). The document summarizes the shooting method for solving boundary value problems (bvps). it begins by introducing numerical methods for solving ordinary differential equations (odes), distinguishing between initial value problems (ivps) and bvps.

Numerical Solutions Of Boundary Value Problems With So Called Shooting However, mathematical models of physical processes often give rise to boundary value problems, where values of the dependent variable(s) are given at points on the boundary of the domain over which the problem is defined. But, what if we could guess a value for the missing initial condition, then integrate towards the second boundary condition using one of our familiar numerical methods, and then adjust our guess if necessary and repeat?. Shooting method for higher order odes and system of odes. a two point boundary value problem for a system of n dimensional odes can be written in the abstract form. The shooting method for boundary value problems consider a boundary value problem of the form y00 = f(x; y; y0); a x b; y(a) = ; y(b) = : (3.1) one natural way to approach this problem is to study the initial value problem (ivp) associated with this di erential equation:.

Solved In The Shooting Method Used To Solve The Boundary Chegg Shooting method for higher order odes and system of odes. a two point boundary value problem for a system of n dimensional odes can be written in the abstract form. The shooting method for boundary value problems consider a boundary value problem of the form y00 = f(x; y; y0); a x b; y(a) = ; y(b) = : (3.1) one natural way to approach this problem is to study the initial value problem (ivp) associated with this di erential equation:. The shooting methods are developed with the goal of transforming the ode boundary value problems to an equivalent initial value problems, then we can solve it using the methods we learned from the previous chapter. The code \ ( non\ lin\ ode.py \) illustrates how our non linear boundary value problem may be solve with a shooting method and offer graphical comparison of the numerical and analytical solution. In the shooting method, we consider the boundary value problem as an initial value problem and try to determine the value y′(a) which results in y(b) = b. finite differences converts the continuous problem to a discrete problem using approximations of the derivative.

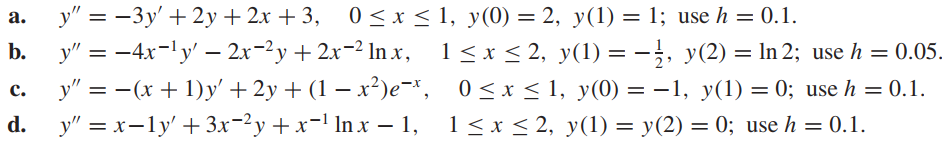
Solved 1 Use The Linear Shooting Method To Approximate The Chegg The shooting methods are developed with the goal of transforming the ode boundary value problems to an equivalent initial value problems, then we can solve it using the methods we learned from the previous chapter. The code \ ( non\ lin\ ode.py \) illustrates how our non linear boundary value problem may be solve with a shooting method and offer graphical comparison of the numerical and analytical solution. In the shooting method, we consider the boundary value problem as an initial value problem and try to determine the value y′(a) which results in y(b) = b. finite differences converts the continuous problem to a discrete problem using approximations of the derivative.

Shooting Method For Boundary Value Problems In the shooting method, we consider the boundary value problem as an initial value problem and try to determine the value y′(a) which results in y(b) = b. finite differences converts the continuous problem to a discrete problem using approximations of the derivative.