Scatterplots And Correlation

Pearson Correlation Coefficient Quick Introduction Learn how to display and interpret the relationship between two quantitative variables using scatterplots and correlation coefficients. see examples, definitions, and facts about correlation and its strength, direction, and form. Master scatterplots & intro to correlation with free video lessons, step by step explanations, practice problems, examples, and faqs. learn from expert tutors and get exam ready!.
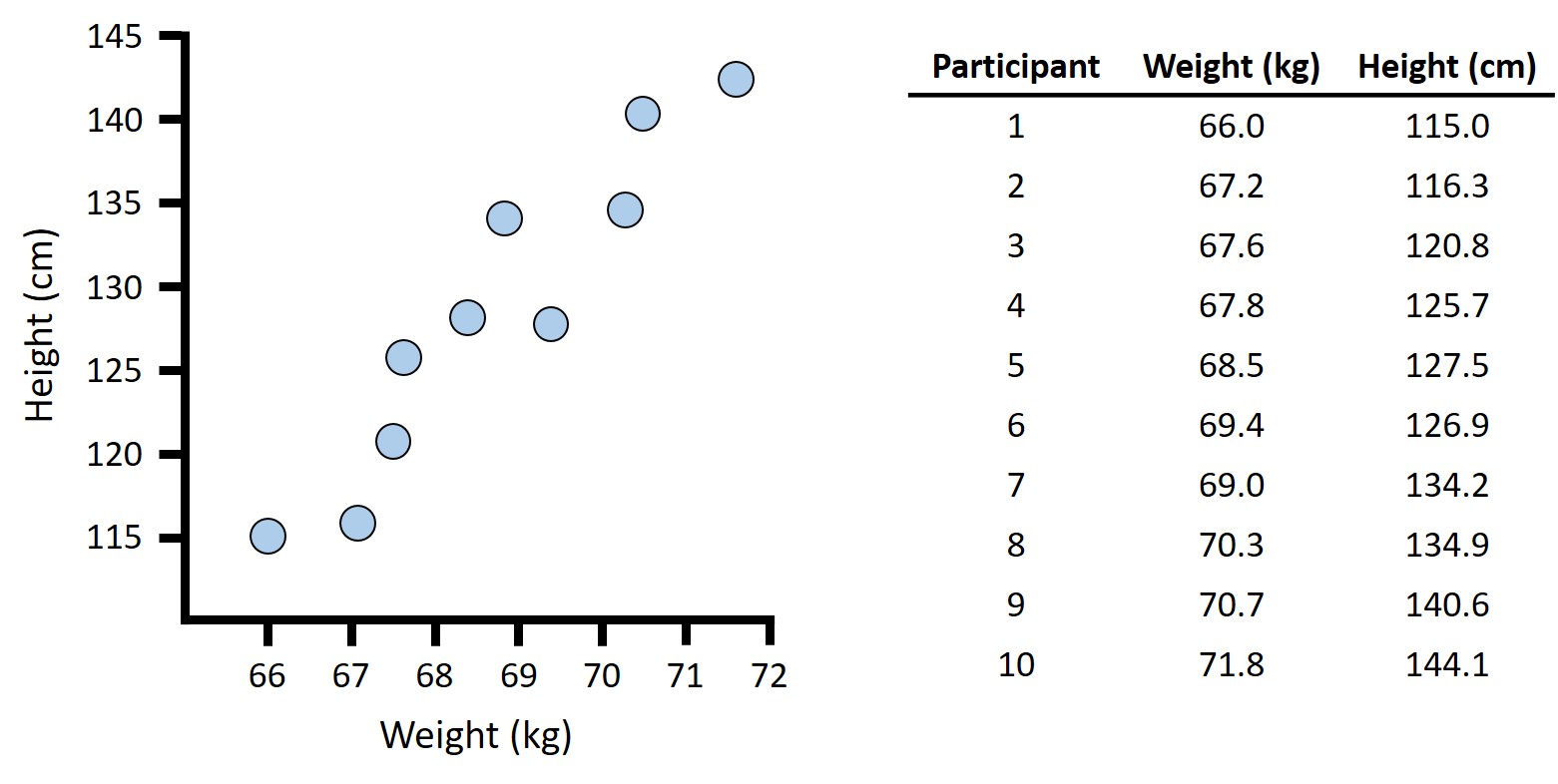
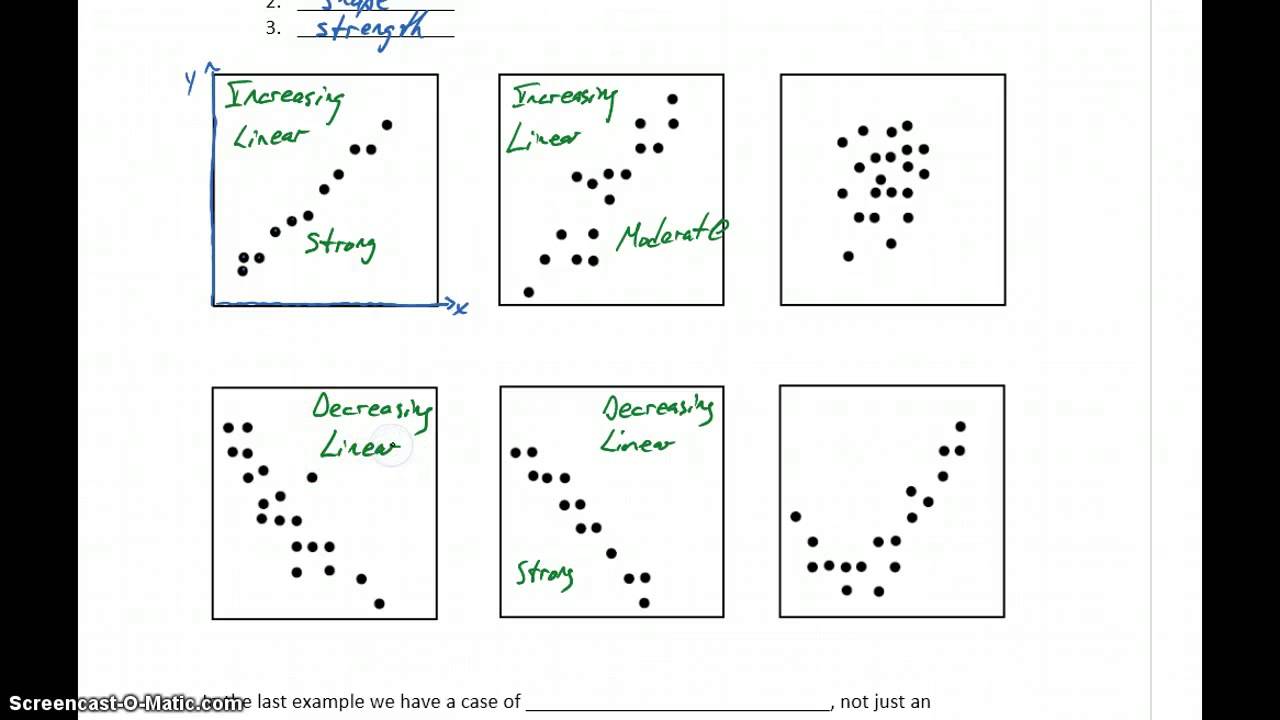
Correlation And Scatterplots Dense or scattered points: if the plotted points are close to each other, then the analyst can expect a high degree of correlation between the two variables. however, if the plotted points are widely scattered, then the analyst can expect a poor correlation between the variables. Scatterplots with no association can have data points scattered across the plot with no discernible pattern or trend. however, it's essential to examine the overall distribution of points to determine whether there's any systematic relationship between the variables or if they're randomly distributed. In this unit you will learn how to create scatterplots and how to calculate pearson’s correlation coefficient with r. you will learn how to enter the code and how to interpret the output that r provides. Besides looking at the scatter plot and seeing that a line seems reasonable, how can you tell if the line is an appropriate model? use the correlation coefficient as another indicator of the strength of the linear relationship between two variables.
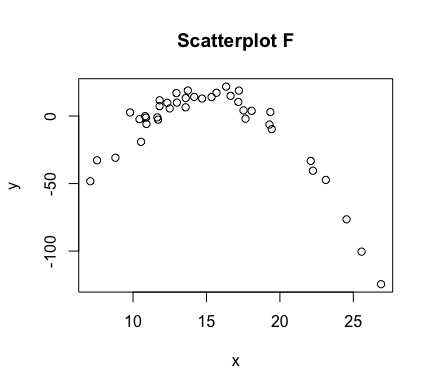
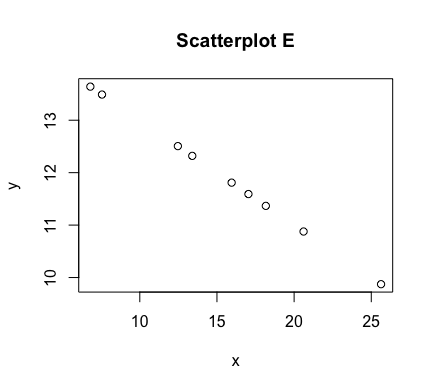
Correlation And Scatterplots In this unit you will learn how to create scatterplots and how to calculate pearson’s correlation coefficient with r. you will learn how to enter the code and how to interpret the output that r provides. Besides looking at the scatter plot and seeing that a line seems reasonable, how can you tell if the line is an appropriate model? use the correlation coefficient as another indicator of the strength of the linear relationship between two variables. Correlation is a numerical measure of the strength and direction of the linear relationship between two quantitative variables. this could give us a more precise measure of the association than scatterplot. correlation coefficient (denoted r) is a number between 1 and 1. Drawing a regression line (line of best fit) allows us to view the correlations between two variables (ie the impact of smoking and drinking on life expectancy). this allows us to identify strong or weak relationships which in turn can influence future decisions within a business. Explore scatter plots in depth to reveal intricate variable correlations with our clear, detailed, and comprehensive visual guide. In figures c and e, we have a perfect linear relationship. in these plots, the correlation is as strong as it can be. scatterplots a and b have correlations that are less strong, with a perhaps being slightly stronger than b. in scatterplot d, there appears to be no correlation at all.
Correlation Scatter Plot Calculator Qerycast Correlation is a numerical measure of the strength and direction of the linear relationship between two quantitative variables. this could give us a more precise measure of the association than scatterplot. correlation coefficient (denoted r) is a number between 1 and 1. Drawing a regression line (line of best fit) allows us to view the correlations between two variables (ie the impact of smoking and drinking on life expectancy). this allows us to identify strong or weak relationships which in turn can influence future decisions within a business. Explore scatter plots in depth to reveal intricate variable correlations with our clear, detailed, and comprehensive visual guide. In figures c and e, we have a perfect linear relationship. in these plots, the correlation is as strong as it can be. scatterplots a and b have correlations that are less strong, with a perhaps being slightly stronger than b. in scatterplot d, there appears to be no correlation at all.
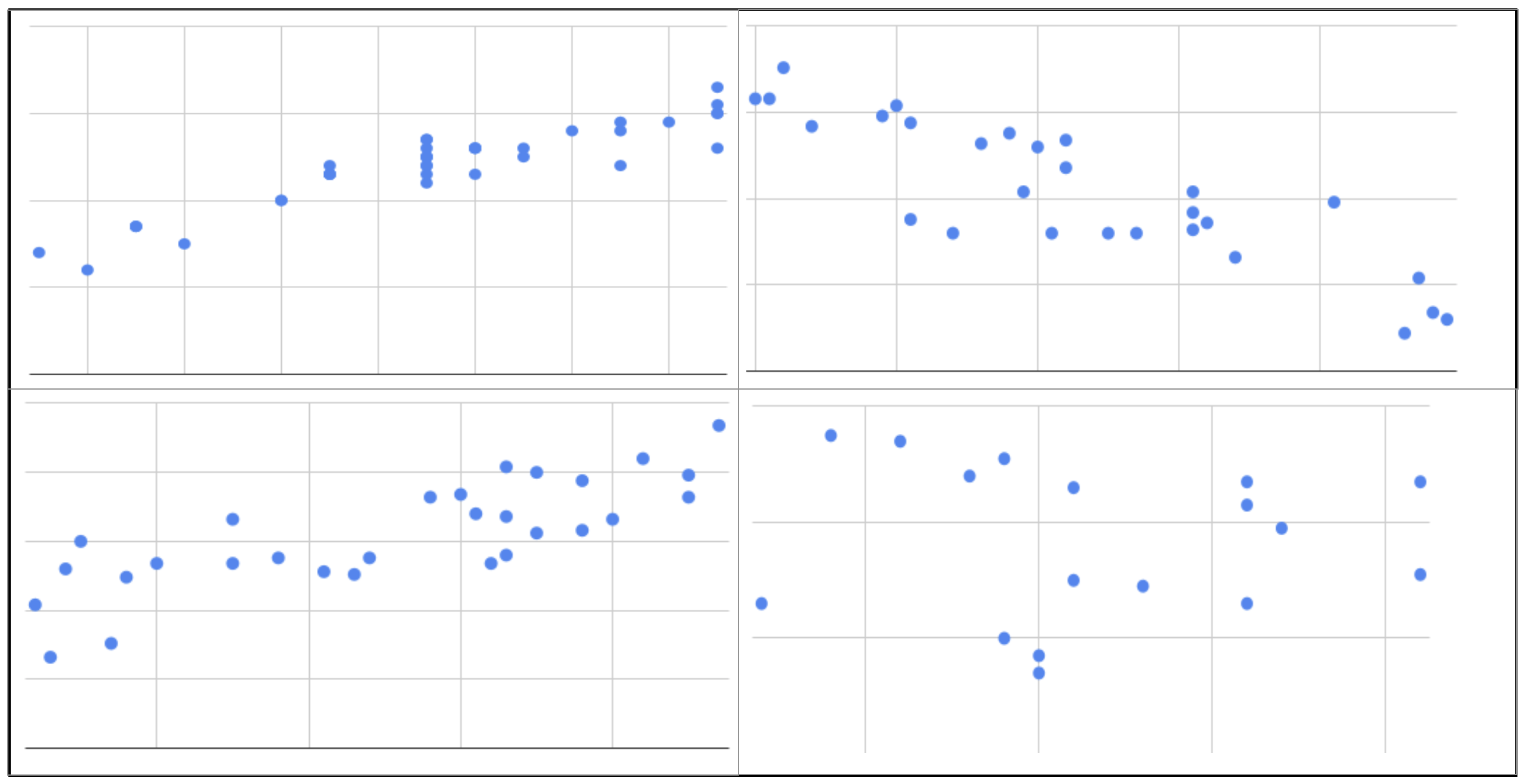
Correlation Introduction To Google Sheets And Sql Explore scatter plots in depth to reveal intricate variable correlations with our clear, detailed, and comprehensive visual guide. In figures c and e, we have a perfect linear relationship. in these plots, the correlation is as strong as it can be. scatterplots a and b have correlations that are less strong, with a perhaps being slightly stronger than b. in scatterplot d, there appears to be no correlation at all.
Scatter Plot Correlation Worksheet E Streetlight
Comments are closed.