Probability Theory And Density Estimation Unsupervised Learning For Big Data

Probability Theory Lecture 14 Pdf The field of unsupervised learning is a collection of methods, and this course is an introduction to several of the most useful techniques, grounded in an intuitive understanding of the. Density estimation is one of the central areas of statistics whose purpose is to estimate the prob ability density function underlying the observed data. it serves as a building block for many tasks in statistical inference, visualization, and machine learning.

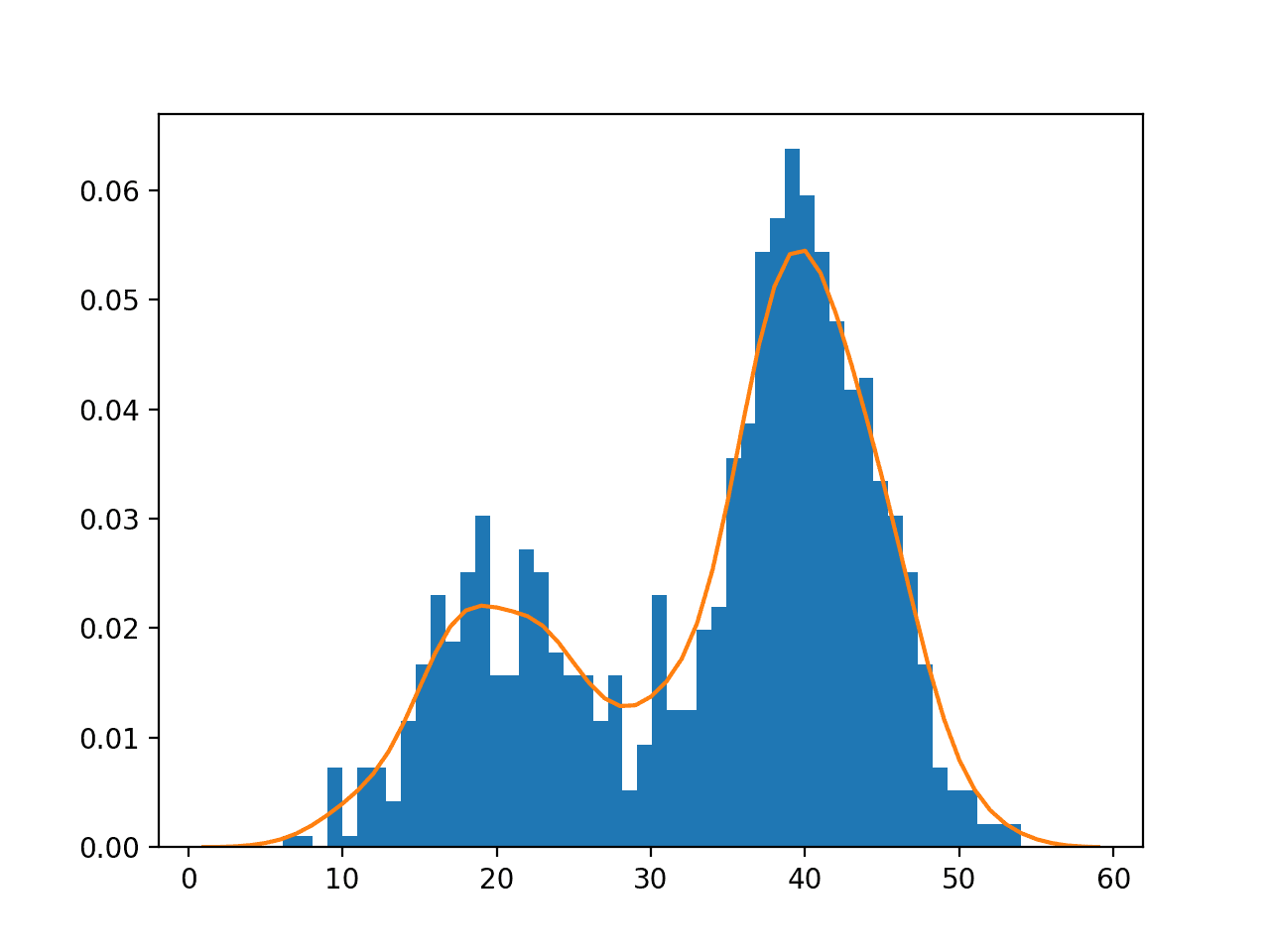
A Gentle Introduction To Probability Density Estimation We used n gaussians centered at fxig, to make weighted averages of y's. in kernel density estimation (kde), use the average of the same n gaussians to estimate the probability density function f(x) which generated the unsupervised (no y) examples fxig. consider the 1d case. our kernel model is n ^fb(x) 1 x = k nb. Part 1: density estimation ¶ density estimation is the problem of estimating a probability distribution from data. as a first step, we will introduce probabilistic models for unsupervised learning. • problem: if there are two different parameter values that are close in terms of the likelihood, using only one of them may introduce a strong bias, if we use it, for example, for predictions. what does it do? • how to use the posterior for modeling p(x)? parameter estimation. coin example. parameter estimation. example. Unsupervised learning for multivariate probability density estimation: radial basis and projection pursuit >.

Pdf Unsupervised Learning Algorithms In Big Data An Overview • problem: if there are two different parameter values that are close in terms of the likelihood, using only one of them may introduce a strong bias, if we use it, for example, for predictions. what does it do? • how to use the posterior for modeling p(x)? parameter estimation. coin example. parameter estimation. example. Unsupervised learning for multivariate probability density estimation: radial basis and projection pursuit >. In practice, scientists often address this through trial and error: plot the data a few times until it looks “right”. but what does it mean for histogram data to look right? there have been a number of solutions proposed to address this problem. This paper reviews a collection of selected nonparametric density estimation algorithms for high dimensional data, some of them are recently published and provide interesting mathematical insights. One can throw away once the histogram is computed. the estimated density has singularities and discontinuities due to the bin edges rather than any property of the underlying density. scales poorly (curse of dimensionality): we would have each variable in a dimensional space into bins. To motivate the use of kernels for density estimation, it helps to see some of the shortcomings of histograms1. a histogram can change signi cantly when changing the position of the bins: kernel methods can accurately estimate any data distribution (non parametric density estimation).

Unsupervised Learning Density Estimation In This Chegg In practice, scientists often address this through trial and error: plot the data a few times until it looks “right”. but what does it mean for histogram data to look right? there have been a number of solutions proposed to address this problem. This paper reviews a collection of selected nonparametric density estimation algorithms for high dimensional data, some of them are recently published and provide interesting mathematical insights. One can throw away once the histogram is computed. the estimated density has singularities and discontinuities due to the bin edges rather than any property of the underlying density. scales poorly (curse of dimensionality): we would have each variable in a dimensional space into bins. To motivate the use of kernels for density estimation, it helps to see some of the shortcomings of histograms1. a histogram can change signi cantly when changing the position of the bins: kernel methods can accurately estimate any data distribution (non parametric density estimation).

Unsupervised Learning Density Estimation In This Chegg One can throw away once the histogram is computed. the estimated density has singularities and discontinuities due to the bin edges rather than any property of the underlying density. scales poorly (curse of dimensionality): we would have each variable in a dimensional space into bins. To motivate the use of kernels for density estimation, it helps to see some of the shortcomings of histograms1. a histogram can change signi cantly when changing the position of the bins: kernel methods can accurately estimate any data distribution (non parametric density estimation).