Por Que Tiemblan Los Ojos

Por Qué Nos Tiemblan Los Ojos Estudio Demostró Cuáles Son Las Causas I know that $\\infty \\infty$ is not generally defined. however, if we have 2 equal infinities divided by each other, would it be 1? if we have an infinity divided by another half as big infinity, for. Soy consciente de que todos, en algún momento, no hemos podido realizar una demostración por nuestra cuenta y hemos tenido que ver la de un libro, un autor o un video. en casos extremos, incluso recurrimos a chatgpt, jajaja.
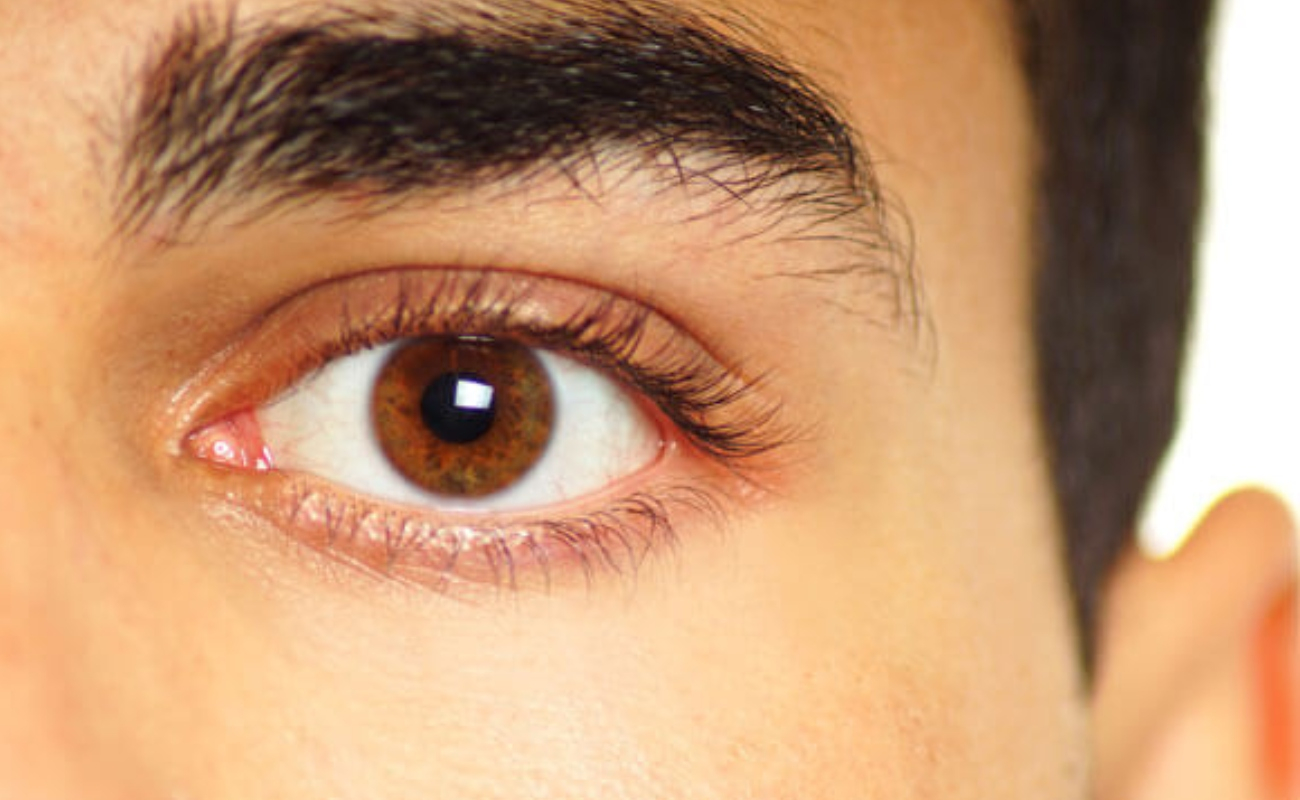
Por Qué Nos Tiemblan Los Ojos Qué Nos Quiere Decir Nuestro Cuerpo In mathematical notation, what are the usage differences between the various approximately equal signs "≈", "≃", and "≅"? the unicode standard lists all of them inside the mathematical operators b. Does anyone have a recommendation for a book to use for the self study of real analysis? several years ago when i completed about half a semester of real analysis i, the instructor used "introducti. Division is the inverse operation of multiplication, and subtraction is the inverse of addition. because of that, multiplication and division are actually one step done together from left to right; the same goes for addition and subtraction. therefore, pemdas and bodmas are the same thing. to see why the difference in the order of the letters in pemdas and bodmas doesn't matter, consider the. The theorem that $\binom {n} {k} = \frac {n!} {k! (n k)!}$ already assumes $0!$ is defined to be $1$. otherwise this would be restricted to $0

Por Qué Tiemblan Los Ojos Estudio Develó Cuáles Son Las Causas Y Cómo Division is the inverse operation of multiplication, and subtraction is the inverse of addition. because of that, multiplication and division are actually one step done together from left to right; the same goes for addition and subtraction. therefore, pemdas and bodmas are the same thing. to see why the difference in the order of the letters in pemdas and bodmas doesn't matter, consider the. The theorem that $\binom {n} {k} = \frac {n!} {k! (n k)!}$ already assumes $0!$ is defined to be $1$. otherwise this would be restricted to $0
Comments are closed.