Modular Exponentiation Tutorial Algorithm
Github Iamsinghashutosh Modular Exponentiation Calculation Of X Y While computing with large numbers modulo, the (%) operator takes a lot of time, so a fast modular exponentiation is used. python has pow (x, e, m) to get the modulo calculated which takes a lot less time. In this video, i discuss the various ways of computing modular exponentiations and provide detailed examples for each of them.

Modular Exponentiation Discrete Mathematical Structures Modular exponentiation is exponentiation performed over a modulus. it is useful in computer science, especially in the field of public key cryptography, where it is used in both diffie–hellman key exchange and rsa public private keys. Raising numbers to large exponents (in mod arithmetic) and finding multiplicative inverses in modular arithmetic are things computers can do quickly. The complete working code is available here. earlier this week i've discussed efficient algorithms for exponentiation. however, for real life needs of number theoretic computations, just raising numbers to large exponents isn't very useful, because extremely huge numbers start appearing very quickly [1], and these don't have much use. Here we show the modular exponentiation algorithm for integers a way to efficiently compute ae (mod n). this general algorithm may also be used for other algebraic structures which have multiplication and exponentiation and is efficient when the size of values has an upper bound the modulus.
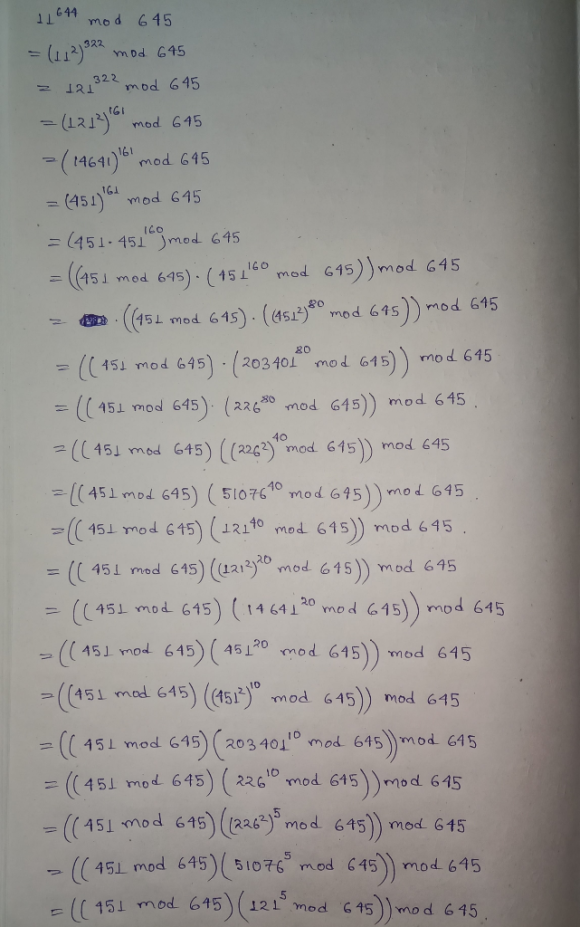
Use Algorithm Modular Exponentiation To Find 11 644 Mod 645 Wizedu The complete working code is available here. earlier this week i've discussed efficient algorithms for exponentiation. however, for real life needs of number theoretic computations, just raising numbers to large exponents isn't very useful, because extremely huge numbers start appearing very quickly [1], and these don't have much use. Here we show the modular exponentiation algorithm for integers a way to efficiently compute ae (mod n). this general algorithm may also be used for other algebraic structures which have multiplication and exponentiation and is efficient when the size of values has an upper bound the modulus. Modular exponentiation is a base fundamental algoritm in number theory and cryptography that works to efficiently find the remainder of an integer raised to a power then divided by another integer. 51 1 32 all, mod 1071. next we calculate 151 raised to the 1, 4, 8, 32. 64, and 128 mod 1071. actually, to get an easier algorithm we will calculate 151 raised to each of the powers of 2 up to 128: 1, 2, 4, 8, 16, 32. 51mod1071 = 631mod1071 in mathematica, this algorithm is i. lemented as po. In this section we will look at some problems involving modular exponentiation and some techniques we can use to solve such problems. suppose we are asked to determine the remainder of the enormous number 1051239203 after dividing it by 5. this number has over 50 million digits!. Learn modular exponentiation with examples and an algorithm. efficiently calculate large exponents modulo a number. number theory worksheet.
Comments are closed.