Modular Arithmetic W 17 Step By Step Examples
Modular Arithmetic W 17 Step By Step Examples 52 Off The clock every time you think about “time,” you use modular arithmetic because it deals with cycles of integers and remainders just like a clock. for example, suppose your clock reads 9:00 (am pm is not important). what will the clock show in 10 hours?. New notion of “sameness” or “equivalence” that will help us understand modular arithmetic. this is a predicate (t f values) on integers . it does not produce numbers as output. there is really a notion of sameness for each > 0 . it may help you to think of ≡ (mod ) for a fixed. > 0 as an equivalence ≡ .

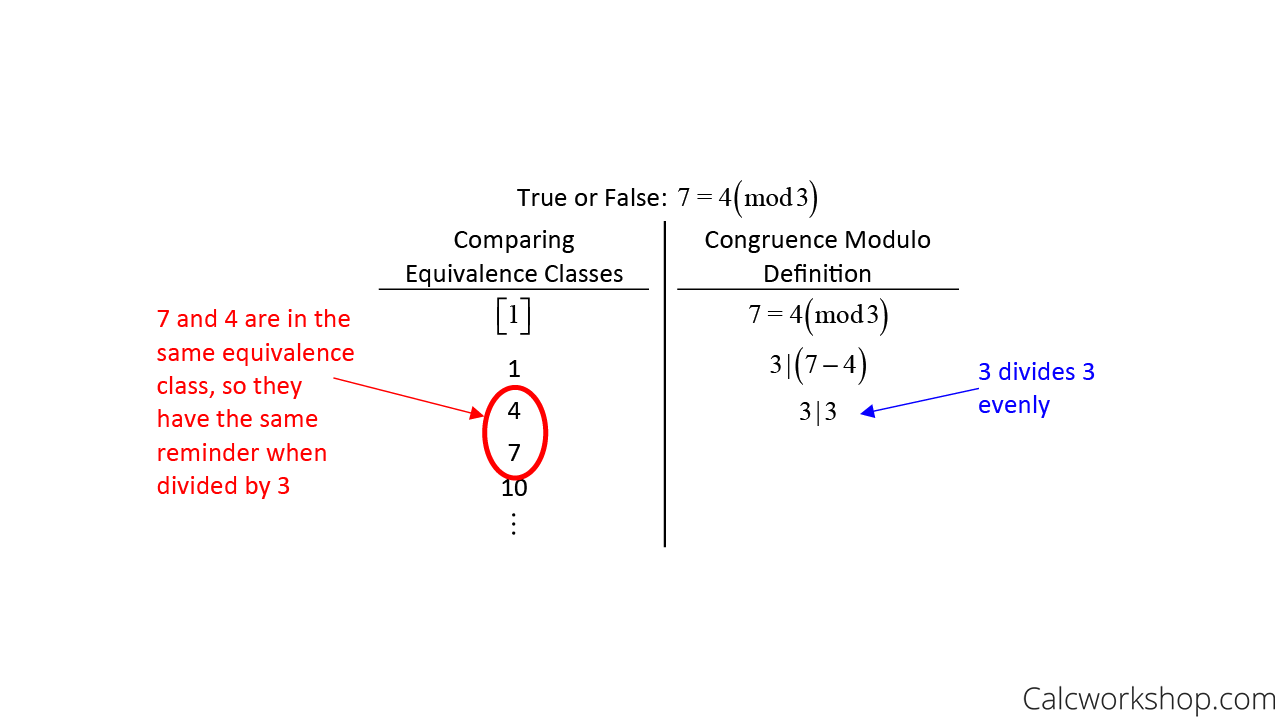
Modular Arithmetic Pdf Abstract Algebra Mathematics Some of the results we derived earlier can be easily proven via modular arithmetic. for example, show that if an integer \ (n\) is not divisible by 3, then \ (n\equiv\pm1\) (mod 3). Modular arithmetic motivates many questions that don’t arise when study ing classic arithmetic. for example, in classic arithmetic, adding a positive number a to another number b always produces a number larger than b. in modular arithmetic this is not always so. This guide will walk you through the fundamentals of modular arithmetic, from basic concepts to practical applications, with clear examples and step by step problem solving techniques. Step support programme assignment 17 warm up 1 this question is about modular arithmetic (and so is the warm down); a very simple idea, but a very important tool in the theory of numbers. we say that n mod a = n.

Modular Arithmetic Pdf Group Mathematics Metric Geometry This guide will walk you through the fundamentals of modular arithmetic, from basic concepts to practical applications, with clear examples and step by step problem solving techniques. Step support programme assignment 17 warm up 1 this question is about modular arithmetic (and so is the warm down); a very simple idea, but a very important tool in the theory of numbers. we say that n mod a = n. Discover how to understand and perform modular arithmetic calculations. learn about modular inverses using the extended euclidean algorithm, simplify expressions with properties, and explore applications in cryptography and real life scenarios like clock arithmetic. It is denoted by so, modular addition let a and b be two integers, and 'm' be a fixed positive integer. then, an 'addition modulo m' b is denoted by a b is defined as the remainder when a b is divided by m. This is the idea behind modular arithmetic, which is sometimes referred to as "clock arithmetic" because 19 mod 12 = 7 mod 12, where 7 represents the remainder when 19 is divided by 12. Here, we provide a detailed step by step guide on performing modular calculations. walk through practical examples that illustrate the application of modular arithmetic, making it easier for both beginners and enthusiasts to grasp.

Modular Arithmetic Part 1 Pdf Pdf Discover how to understand and perform modular arithmetic calculations. learn about modular inverses using the extended euclidean algorithm, simplify expressions with properties, and explore applications in cryptography and real life scenarios like clock arithmetic. It is denoted by so, modular addition let a and b be two integers, and 'm' be a fixed positive integer. then, an 'addition modulo m' b is denoted by a b is defined as the remainder when a b is divided by m. This is the idea behind modular arithmetic, which is sometimes referred to as "clock arithmetic" because 19 mod 12 = 7 mod 12, where 7 represents the remainder when 19 is divided by 12. Here, we provide a detailed step by step guide on performing modular calculations. walk through practical examples that illustrate the application of modular arithmetic, making it easier for both beginners and enthusiasts to grasp.
Comments are closed.