Modular Arithmetic Modulo 12 Addition

Modulo Arithmetic Pdf This goal of this article is to explain the basics of modular arithmetic while presenting a progression of more difficult and more interesting problems that are easily solved using modular arithmetic. Clear visualisation of addition in modulo 12 (mod 12) showing why modular arithmetic is also called clock arithmetic. subtitles available.
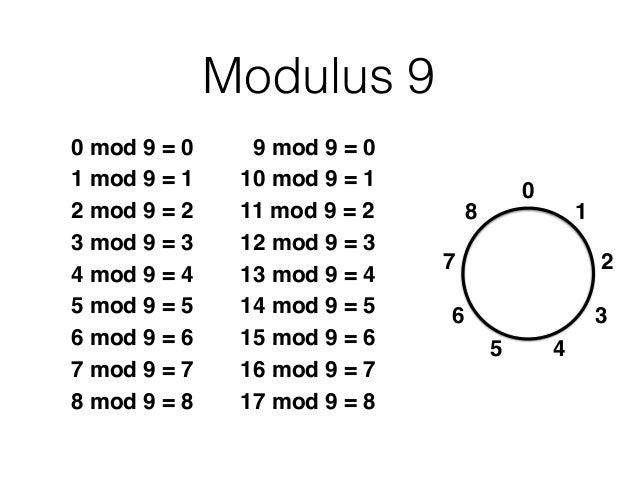
Modular Arithmetic Addition And Subtraction Fill in the addition and multiplication tables below in mod n, where n = 4, n = 5, and n = 7. be sure to reduce all the numbers in the appropriate mod arithmetic. In arithmetic modulo n, when we add, subtract, or multiply two numbers, we take the answer mod n. for example, if we want the product of two numbers modulo n, then we multiply them normally and the answer is the remainder when the normal product is divided by n. To add or subtract in mod 12, perform the calculation in the usual manner (7 15 = 22) and then add or subtract 12′s until you get a number from 0 to 11 (22 12 = 10). To add or subtract in mod12, perform the calculation in the usual manner (7 15 = 22) and then add or subtract 12s until you get a number from 0 to 11 (22 12 = 10).

Modular Arithmetic To add or subtract in mod 12, perform the calculation in the usual manner (7 15 = 22) and then add or subtract 12′s until you get a number from 0 to 11 (22 12 = 10). To add or subtract in mod12, perform the calculation in the usual manner (7 15 = 22) and then add or subtract 12s until you get a number from 0 to 11 (22 12 = 10). The study of the properties of the system of remainders is called modular arithmetic. it is an essential tool in number theory. 2.1. definition of z nz in this section we give a careful treatment of the system called the integers modulo (or mod) n. 2.1.1 definition let a, b ∈ z and let n ∈ n. Addition and subtraction properties of addition in modular arithmetic: if a b = c, then a (mod n) b (mod n) ≡ c (mod n). if a ≡ b (mod n), then a k ≡ b k (mod n) for any integer k. if a ≡ b (mod n), and c ≡ d (mod n), then a c ≡ b d (mod n). if a ≡ b (mod n), then − a ≡ − b (mod n). Operations can be done using modular arithmetic. the teacher explains the lesson. the sum of two integers in a given modular system is obtained by adding two int. gers and then finding the remainder when the sum is divided by the given modulus. similarly, the difference between two integers is o.

Modular Arithmetic Addition And Subtraction The study of the properties of the system of remainders is called modular arithmetic. it is an essential tool in number theory. 2.1. definition of z nz in this section we give a careful treatment of the system called the integers modulo (or mod) n. 2.1.1 definition let a, b ∈ z and let n ∈ n. Addition and subtraction properties of addition in modular arithmetic: if a b = c, then a (mod n) b (mod n) ≡ c (mod n). if a ≡ b (mod n), then a k ≡ b k (mod n) for any integer k. if a ≡ b (mod n), and c ≡ d (mod n), then a c ≡ b d (mod n). if a ≡ b (mod n), then − a ≡ − b (mod n). Operations can be done using modular arithmetic. the teacher explains the lesson. the sum of two integers in a given modular system is obtained by adding two int. gers and then finding the remainder when the sum is divided by the given modulus. similarly, the difference between two integers is o.

Modulo Arithmetic Addition Variation Theory Operations can be done using modular arithmetic. the teacher explains the lesson. the sum of two integers in a given modular system is obtained by adding two int. gers and then finding the remainder when the sum is divided by the given modulus. similarly, the difference between two integers is o.
Comments are closed.