Math Example Systems Of Equations Solving Linear Systems By

Math Example Systems Of Equations Solving Linear Systems By In this section, we’ll look at some specific types of applications that relate two quantities. we’ll translate the words into linear equations, decide which is the most convenient method to use, and then solve them. we will use our problem solving strategy for systems of linear equations. We can solve systems of two equations using three main methods: elimination, substitution, and graphical methods. here, we will focus on the elimination method and the substitution method. we can follow the following steps to solve the system by substitution:.

Math Example Systems Of Equations Solving Linear Systems By Linear systems with three variables – in this section we will work a couple of quick examples illustrating how to use the method of substitution and method of elimination introduced in the previous section as they apply to systems of three equations. College algebra lecture 32 systems of linear equations in this lecture, we learn about systems of linear equations, solving them by substitution and elimination. Here is everything you need to know about solving systems of linear equations. you will learn what systems of equations are and how to solve them graphically and algebraically. students first learn about systems of equations in grade 8 and expand their knowledge as they progress through high school mathematics. what are systems of equations?. What are systems of linear equations. learn its general form and how to solve them involving two or more variables with examples.
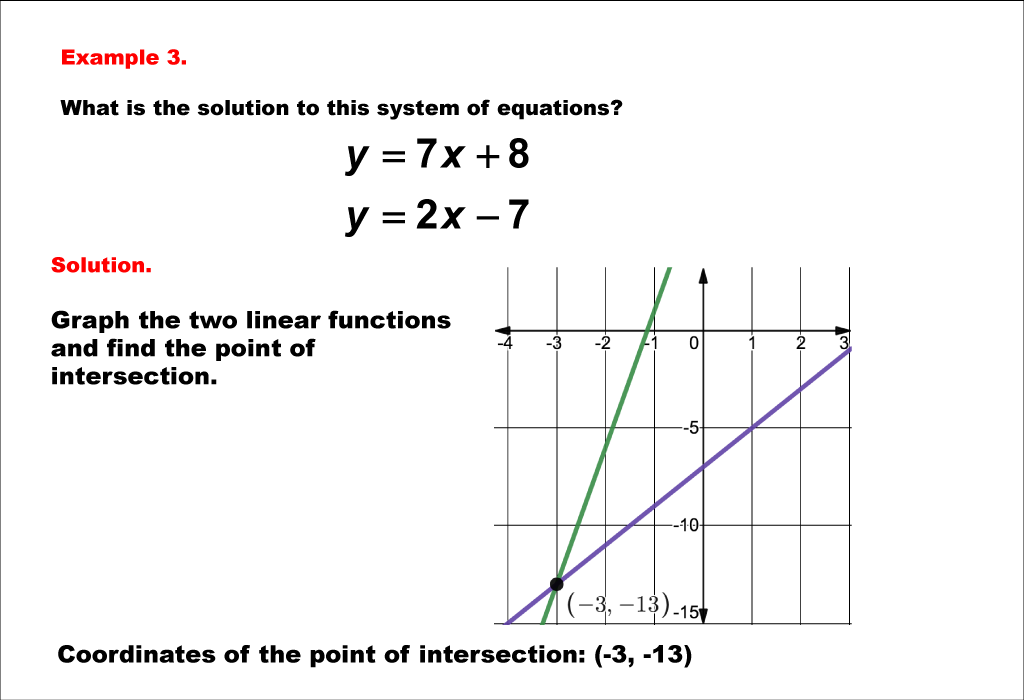
Math Example Systems Of Equations Solving Linear Systems By Graphing Here is everything you need to know about solving systems of linear equations. you will learn what systems of equations are and how to solve them graphically and algebraically. students first learn about systems of equations in grade 8 and expand their knowledge as they progress through high school mathematics. what are systems of equations?. What are systems of linear equations. learn its general form and how to solve them involving two or more variables with examples. The solution to a system of linear equations in two variables is any ordered pair that satisfies each equation independently. in the above example, the order pair (4,7) is the solution to the system of equations 2(4) 7 = 15. In this section, you will learn how to solve systems of linear equations using many methods. here are the sections within this page: if we look at the coefficients on a single letter between the two equations and they are opposites of each other, then we can add the two equations to cancel that letter. This section combines ideas from section 0.5 and section 1.3.1 so that we can start to solve systems of linear equations. before we get ahead of ourselves, let’s review a few definitions. There are two basic methods of solving linear systems algebraically: the substitution method and the elimination method (addition subtraction method).
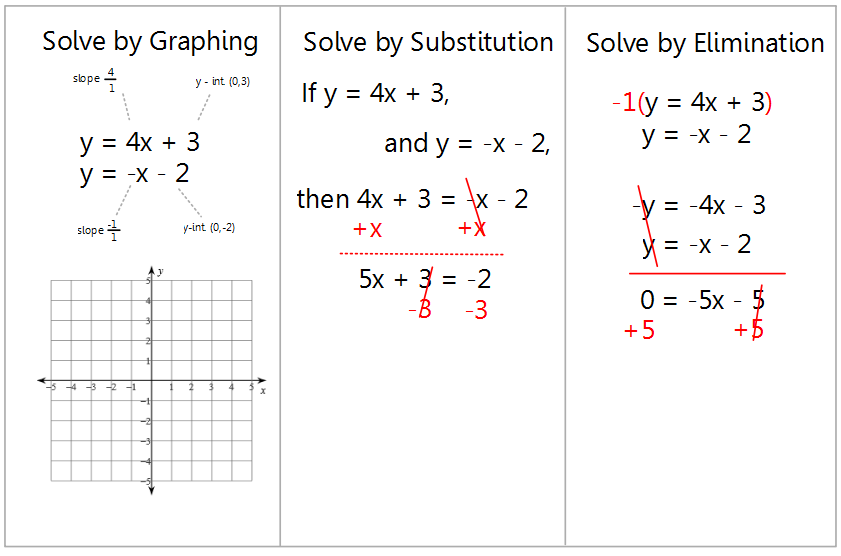
Math Example Systems Of Equations Solving Linear Systems By The solution to a system of linear equations in two variables is any ordered pair that satisfies each equation independently. in the above example, the order pair (4,7) is the solution to the system of equations 2(4) 7 = 15. In this section, you will learn how to solve systems of linear equations using many methods. here are the sections within this page: if we look at the coefficients on a single letter between the two equations and they are opposites of each other, then we can add the two equations to cancel that letter. This section combines ideas from section 0.5 and section 1.3.1 so that we can start to solve systems of linear equations. before we get ahead of ourselves, let’s review a few definitions. There are two basic methods of solving linear systems algebraically: the substitution method and the elimination method (addition subtraction method).
Comments are closed.