Markov Chains Course Week 5 Lecture 1

Markov Chains Course Week 5 Lecture 1 In this section we give the definition of a markov chain and several related concepts. Example 1. a colleague travels between four coee shops located as follows: 3 4 ach path as equally likely. if we model our colleague’s journey as a markov chain, then a suitable state space would be s = {1, 2, 3, 4} and the transition 0 1 0 0 = p 1 3.

Markov Chains Course Week 5 Lecture 1 There are 2 examples sheets, each containing 13 questions, as well as 3 or 4 "extra" optional questions. the extra questions are interesting and off the well beaten path of questions that are typical for an introductory markov chains course. you should receive a supervision on each examples sheet. This course is an introduction to markov chains, random walks, martingales. course : monday and wednesday, 11 :00 am 12 :30pm. 5 homeworks (10% each) midterm (15%, april 1st.) final (35%, may) homeworks will be collected at the end of the class on the due date. In order to represent the weather in our example as a markov chain, we need to perform a trick that is sometimes called markovian lift. the idea is to consider the weather on two consecutive days together. We can turn any markov chain into an aperiodic markov chain by adding constant steps. consider the new transition probabilities ep(x, y) = ( 1 2 p(x, y), x̸ = y 12 1 2 p(x, x), x= y.

Markov Chains Course Week 5 Lecture 1 In order to represent the weather in our example as a markov chain, we need to perform a trick that is sometimes called markovian lift. the idea is to consider the weather on two consecutive days together. We can turn any markov chain into an aperiodic markov chain by adding constant steps. consider the new transition probabilities ep(x, y) = ( 1 2 p(x, y), x̸ = y 12 1 2 p(x, x), x= y. De nition 1.1 a sequence of random variables (xn) is called a markov chain if the past and future of the process are conditionally independent given the present. The document provides examples of applying these concepts to analyze markov chains and calculate probabilities related to first visit times and state occupancy. In this course, we will consider discrete state stochastic processes such as markov chain, branching chain, poisson process, renewal process, and continuous time markov chain. the first two are discrete time process and the last three are continuous time process.

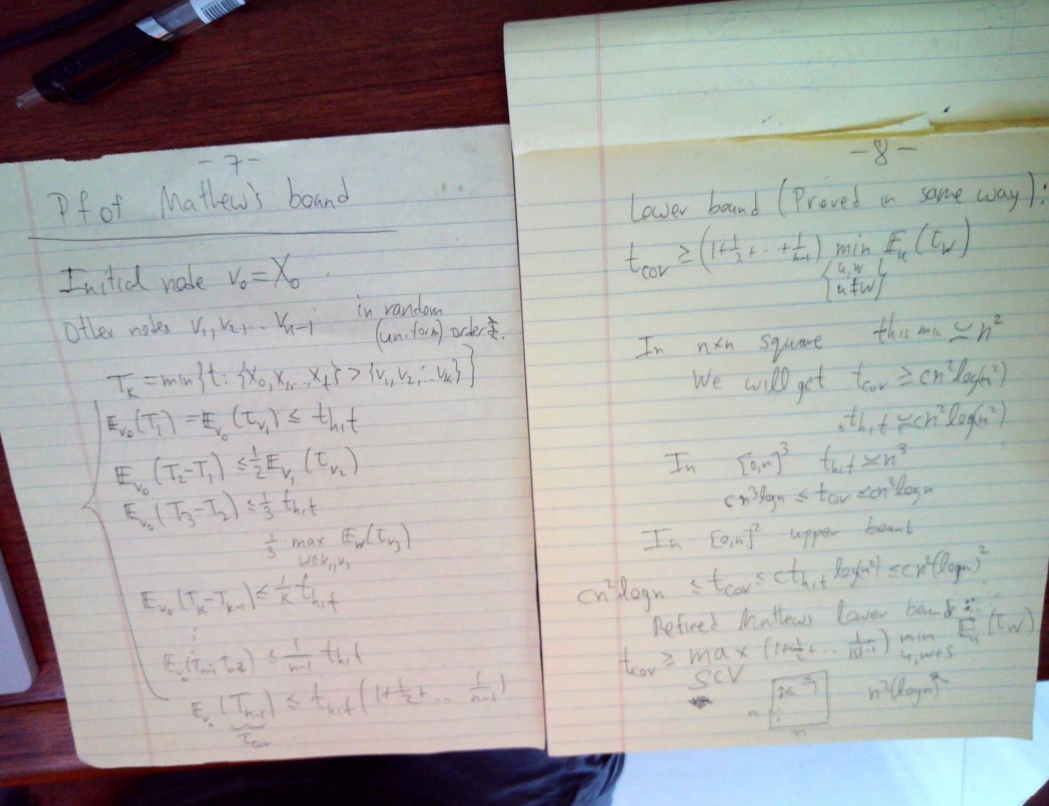
Markov Chains Course Week 5 Lecture 1 De nition 1.1 a sequence of random variables (xn) is called a markov chain if the past and future of the process are conditionally independent given the present. The document provides examples of applying these concepts to analyze markov chains and calculate probabilities related to first visit times and state occupancy. In this course, we will consider discrete state stochastic processes such as markov chain, branching chain, poisson process, renewal process, and continuous time markov chain. the first two are discrete time process and the last three are continuous time process.

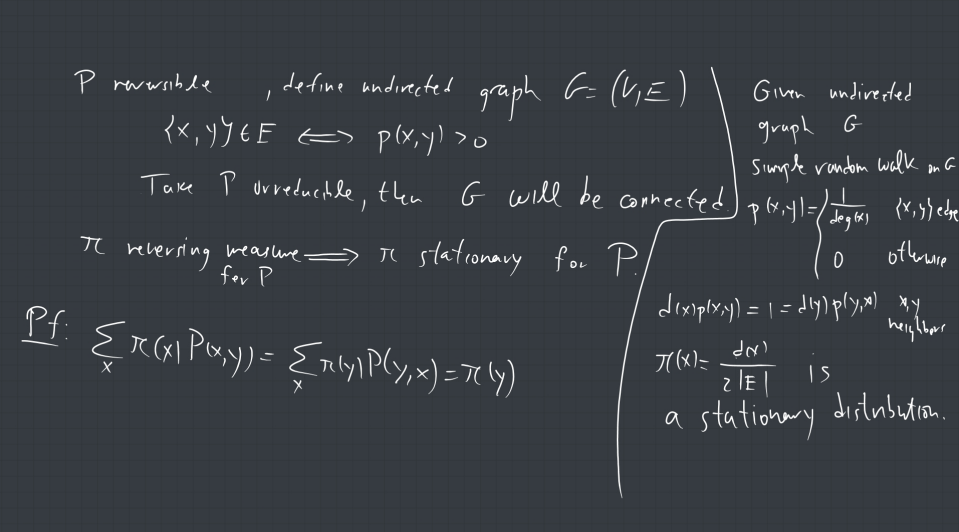
Week 1 Lecture 1 Markov Chains Course In this course, we will consider discrete state stochastic processes such as markov chain, branching chain, poisson process, renewal process, and continuous time markov chain. the first two are discrete time process and the last three are continuous time process.