Lesson 6 Calculating Volume With The Disk Method Part 3

Lesson 6 Calculating Volume With The Disk Method Part 3 Calc 1 This is just a few minutes of a complete course. get full lessons & more subjects at: mathtutordvd . In this lesson, the student will gain extra practice with using the disk method of integrating volumes in calculus. this is just a few minutes from a multi hour course. view the full course and learn by working problems step by step!.

Lesson 4 Calculating Volume With The Disk Method Part 1 Calc 1 The main difference between the volume by discs and volume by shells approaches is the geometric shapes used to approximate the solid. volume by discs utilizes disks perpendicular to the axis of revolution, whereas volume by shells uses cylindrical shells parallel to the axis of revolution. Learn how to use the disk method to find the volume of the solid generated by revolving a bounded region about a horizontal or vertical line. Given an arbitrary solid, we can approximate its volume by cutting it into n thin slices. when the slices are thin, each slice can be approximated well by a general right cylinder. thus the volume of each slice is approximately its cross sectional area × thickness. Find the volume of a solid with known cross sections. revolving regions about a given horizontal line produces a volume with infinitesimally thin circular (or disk shaped) cross sections. the.
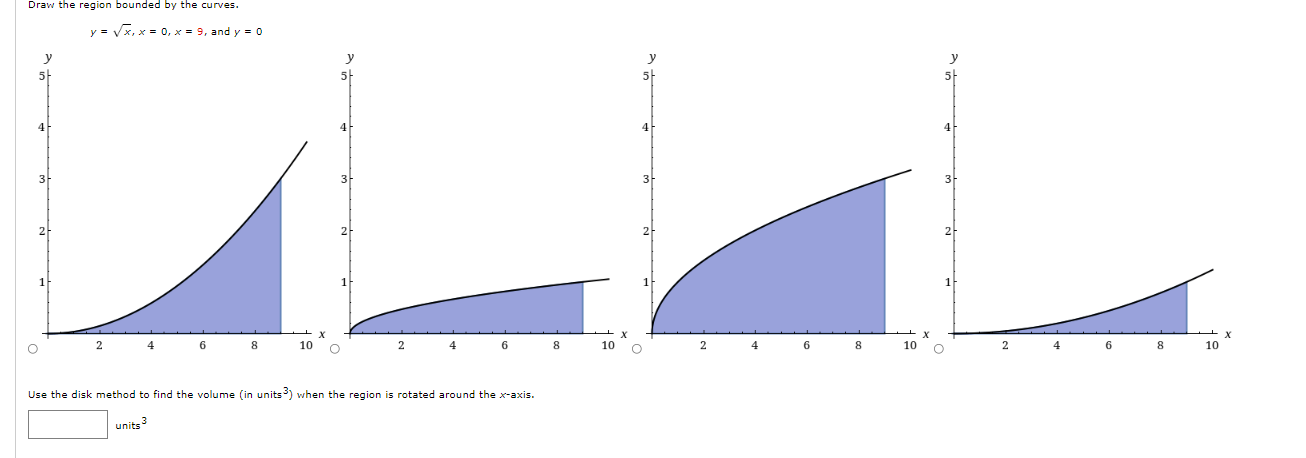
Solved Use The Disk Method To Find The Volume In Units 3 Chegg Given an arbitrary solid, we can approximate its volume by cutting it into n thin slices. when the slices are thin, each slice can be approximated well by a general right cylinder. thus the volume of each slice is approximately its cross sectional area × thickness. Find the volume of a solid with known cross sections. revolving regions about a given horizontal line produces a volume with infinitesimally thin circular (or disk shaped) cross sections. the. The disk method consists on adding the volumes of the disks thus obtained, and then taking the limit as the number of disks goes to infinity. to accomplish this, we first put the formula to compute the volume of a disk in this context. In this section, we explore how to find the volume of a three dimensional solid using integrals, building on the concept of calculating area under a curve. instead of summing up rectangles as in two dimensions, we will slice the solid into thin sections to analyze its volume. This method of finding volume is called the disk method. each disk is formed from one of the rectangles from integration, with the radius coming from the function itself. Volume (the disk washer method) [additional examples] (stewart, chapter 6) (1) compute the volume of the solid obtained by rotating the region enclosed by y = x 4 and y = x about the line y = 1. 1.
Volume Disk Method By Math Powerpoint Lessons Tpt The disk method consists on adding the volumes of the disks thus obtained, and then taking the limit as the number of disks goes to infinity. to accomplish this, we first put the formula to compute the volume of a disk in this context. In this section, we explore how to find the volume of a three dimensional solid using integrals, building on the concept of calculating area under a curve. instead of summing up rectangles as in two dimensions, we will slice the solid into thin sections to analyze its volume. This method of finding volume is called the disk method. each disk is formed from one of the rectangles from integration, with the radius coming from the function itself. Volume (the disk washer method) [additional examples] (stewart, chapter 6) (1) compute the volume of the solid obtained by rotating the region enclosed by y = x 4 and y = x about the line y = 1. 1.
Comments are closed.