Isometry Explained Guide W 9 Step By Step Examples

Isometry Drawception Isometries can be classified as either direct or opposite, but more on that later. in the diagram below, both the image and the preimage of $$\triangle abc $$ have the same dimensions, showing that reflections are isometries. Some examples of common isometry are translation, reflection, rotation, and central symmetry. in this chapter, we will deal with reflection, central symmetry, translation and rotation.

Isometry Explained Guide W 9 Step By Step Examples Isometry is a geometric transformation that preserves the distances between points. in simpler terms, if two points have a certain distance between them before the transformation, that distance remains unchanged afterward. this implies that every isometry maps a figure onto a congruent figure. Rn, we say that s preserves distance when. for all x; y 2 rn. an isometry on rn is an invertible map s : rn ! rn which preserves distance. the set of all isometries on rn is denoted by isom(rn). r is a group under composition. proof: the identity map i : rn ! rn is an isometry because i(x) i(y) = kx yk for all x; y 2 rn. In mathematics, an isometry (or congruence, or congruent transformation) is a distance preserving transformation between metric spaces, usually assumed to be bijective. [a] the word isometry is derived from the ancient greek: ἴσος isos meaning "equal", and μέτρον metron meaning "measure". Step 1: an isometry is a transformation in which the original figure and its image are congruent. step 2: a reflection flips the figure across a line. the new figure is a mirror image of the original figure. step 3: figure 2 is a reflection of figure 1 and figure 3 is a reflection of figure 2.
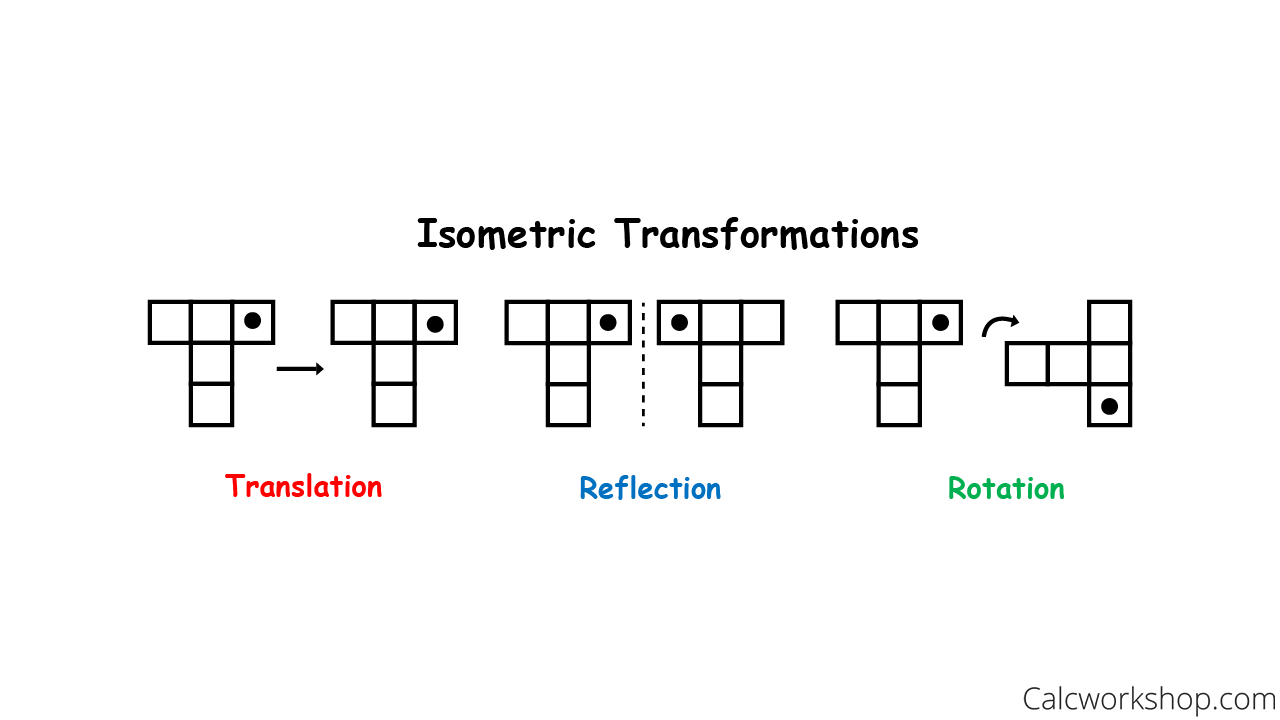
Isometry Explained Guide W 9 Step By Step Examples In mathematics, an isometry (or congruence, or congruent transformation) is a distance preserving transformation between metric spaces, usually assumed to be bijective. [a] the word isometry is derived from the ancient greek: ἴσος isos meaning "equal", and μέτρον metron meaning "measure". Step 1: an isometry is a transformation in which the original figure and its image are congruent. step 2: a reflection flips the figure across a line. the new figure is a mirror image of the original figure. step 3: figure 2 is a reflection of figure 1 and figure 3 is a reflection of figure 2. The first three files demonstrate the three basic isometries. the next three are “mystery isometries”. you could use them now, or save them for the end of the lesson. ask the students to guess which basic isometry is represented in each case, and perhaps have them vote on it. It introduces the concept of isometries, provides examples like identity, reflection, rotation, and translation, and discusses their properties. the video also covers several theorems related to isometries, offering proof techniques and exercises to enhance understanding. The word isometry is derived from the ancient greek: ἴσος isos meaning "equal", and μέτρον metron meaning "measure". if the transformation is from a metric space to itself, it is a kind of geometric transformation known as a motion.
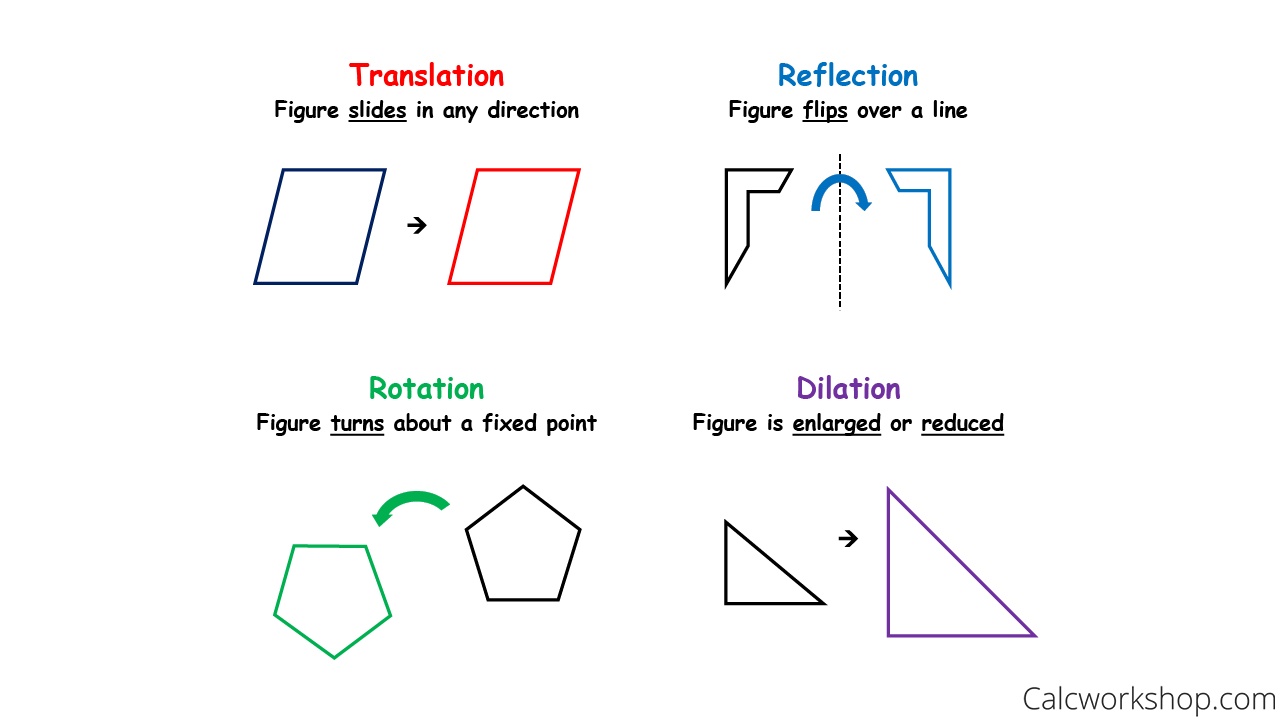
Isometry Explained Guide W 9 Step By Step Examples The first three files demonstrate the three basic isometries. the next three are “mystery isometries”. you could use them now, or save them for the end of the lesson. ask the students to guess which basic isometry is represented in each case, and perhaps have them vote on it. It introduces the concept of isometries, provides examples like identity, reflection, rotation, and translation, and discusses their properties. the video also covers several theorems related to isometries, offering proof techniques and exercises to enhance understanding. The word isometry is derived from the ancient greek: ἴσος isos meaning "equal", and μέτρον metron meaning "measure". if the transformation is from a metric space to itself, it is a kind of geometric transformation known as a motion.
Comments are closed.