Integral Of The Day 8 19 25 Calc 2 Integral Solved Step By Step
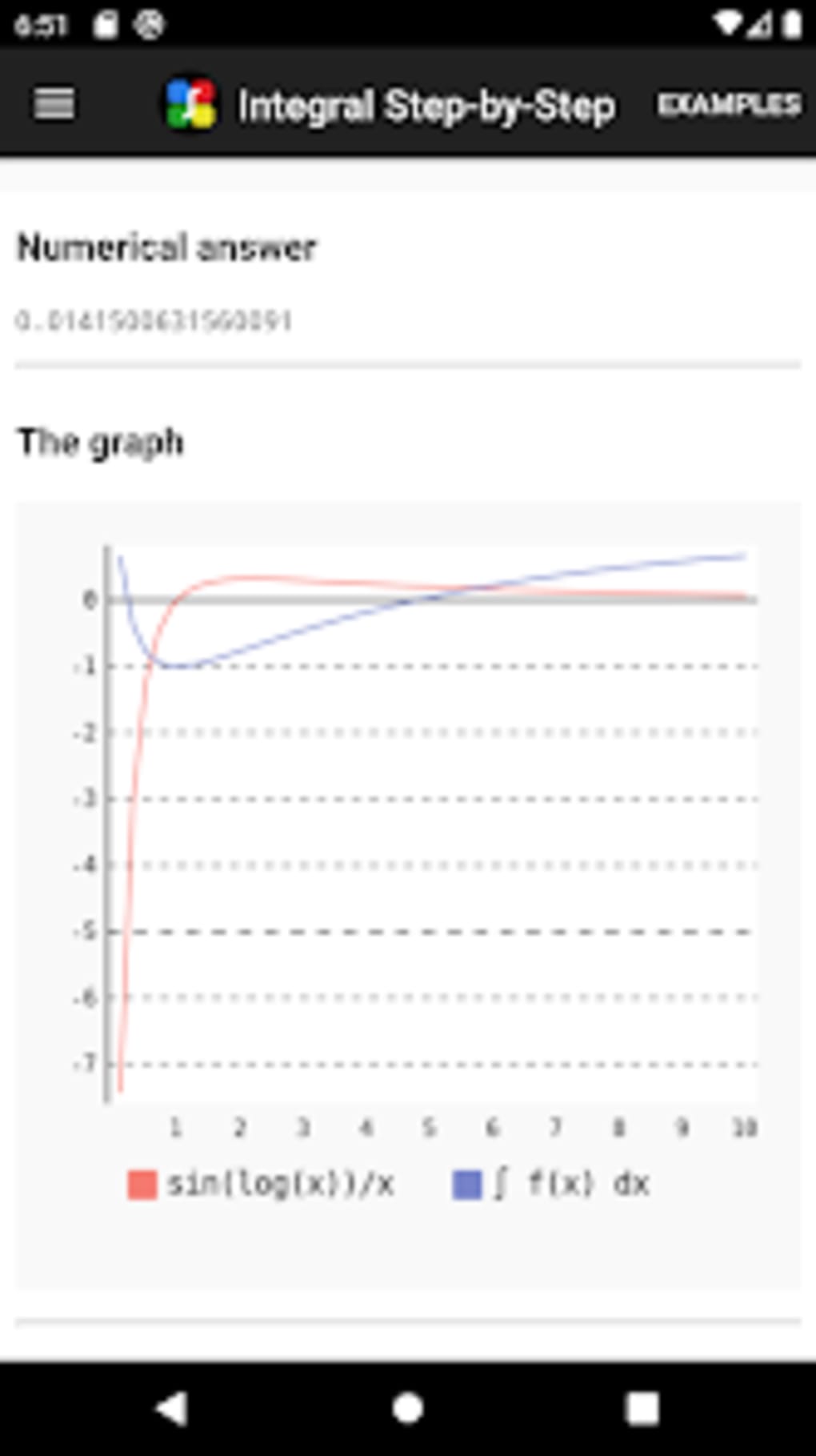
Integral Step By Step Calc For Android Download The integral which you describe has no closed form which is to say that it cannot be expressed in elementary functions. for example, you can express $\int x^2 \mathrm {d}x$ in elementary functions such as $\frac {x^3} {3} c$. I was trying to do this integral $$\int \sqrt {1 x^2}dx$$ i saw this question and its' use of hyperbolic functions. i did it with binomial differential method since the given integral is in a form o.

Integral Step By Step Calc For Android Download Answers to the question of the integral of $\frac {1} {x}$ are all based on an implicit assumption that the upper and lower limits of the integral are both positive real numbers. The improper integral $\int a^\infty f (x) \, dx$ is called convergent if the corresponding limit exists and divergent if the limit does not exist. while i can understand this intuitively, i have an issue with saying that the mathematical object we defined as improper integrals is "convergent" or "divergent". You will get the same answer because when you perform a change of variables, you change the limits of your integral as well (integrating in the complex plane requires defining a contour, of course, so you'll have to be careful about this). The integral of 0 is c, because the derivative of c is zero. also, it makes sense logically if you recall the fact that the derivative of the function is the function's slope, because any function f (x)=c will have a slope of zero at point on the function.

Integral Calculator With Steps Pdf You will get the same answer because when you perform a change of variables, you change the limits of your integral as well (integrating in the complex plane requires defining a contour, of course, so you'll have to be careful about this). The integral of 0 is c, because the derivative of c is zero. also, it makes sense logically if you recall the fact that the derivative of the function is the function's slope, because any function f (x)=c will have a slope of zero at point on the function. 0 the integral of r (d (theta)) from 0 to 2π is 2πr (the circumference of a circle with radius r), now integrate 2πr (dr) from 0 to r and the answer is πr^2 (the area of a circle of radius r). this is my derivation. I was reading on in this article about the n dimensional and functional generalization of the gaussian integral. in particular, i would like to understand how the following equations are. If by integral you mean the cumulative distribution function $\phi (x)$ mentioned in the comments by the op, then your assertion is incorrect. How do you know it's legal to switch the summation and the integral? i know you can do it with finite sums but i thought there were certain conditions under which it invalid to switch them.

Integral Calculator With Steps Download Free Pdf Integral 0 the integral of r (d (theta)) from 0 to 2π is 2πr (the circumference of a circle with radius r), now integrate 2πr (dr) from 0 to r and the answer is πr^2 (the area of a circle of radius r). this is my derivation. I was reading on in this article about the n dimensional and functional generalization of the gaussian integral. in particular, i would like to understand how the following equations are. If by integral you mean the cumulative distribution function $\phi (x)$ mentioned in the comments by the op, then your assertion is incorrect. How do you know it's legal to switch the summation and the integral? i know you can do it with finite sums but i thought there were certain conditions under which it invalid to switch them.

Solution Integral Ex 8 4 Integration Integral Solved Exercise 8 4 If by integral you mean the cumulative distribution function $\phi (x)$ mentioned in the comments by the op, then your assertion is incorrect. How do you know it's legal to switch the summation and the integral? i know you can do it with finite sums but i thought there were certain conditions under which it invalid to switch them.
Comments are closed.