How To Use Second Shifting Theorem For Solving Problems

By healtycares On Aug 25, 2025

The Second Shift Theorem Pdf Laplace Transform Calculus Here we’ll develop procedures to find laplace transforms of piecewise continuous functions, and to find the piecewise continuous inverses of laplace transforms, which will allow us to solve these initial value problems. How to use second shifting theorem for solving problems?.

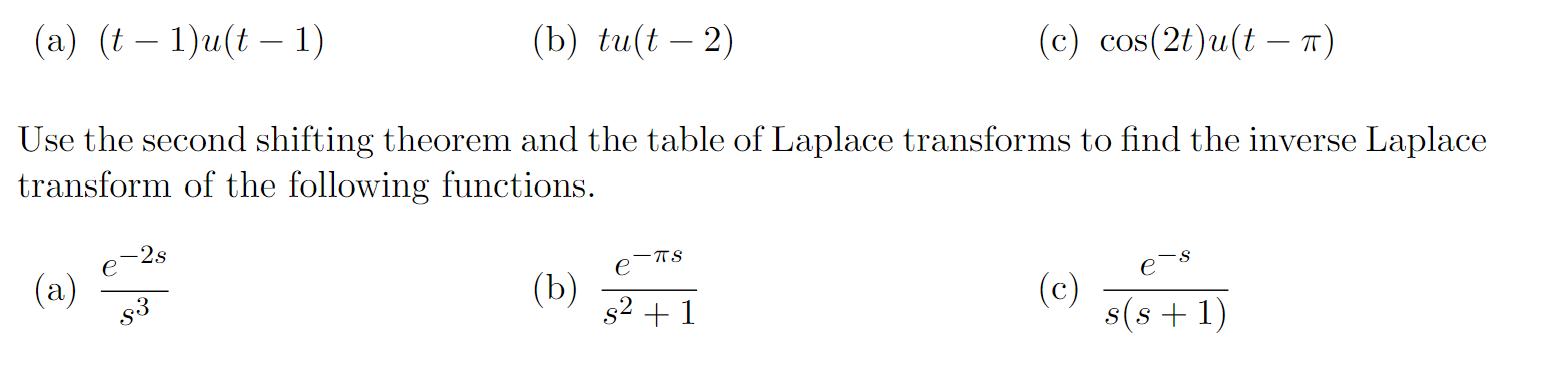
Solved Explain What Is The Second Shifting Theorem And How Chegg Here we calculate the laplace transform of a particular function via the “second shifting theorem”. this video may be thought of as a basic example. Not quite the form we need for the second shifting theorem, but we can apply the good ol' "add zero" trick:. How does the second shifting theorem aid in solving problems involving delayed systems? the second shifting theorem helps solve problems with delayed systems by providing a method to incorporate time shifts directly into the laplace transform. We'll start by introducing the second shifting theorem and explaining how it works. then, we'll walk you through some practical examples of problems that can be solved using this.

Solved Use The Second Shifting Theorem To Find Chegg How does the second shifting theorem aid in solving problems involving delayed systems? the second shifting theorem helps solve problems with delayed systems by providing a method to incorporate time shifts directly into the laplace transform. We'll start by introducing the second shifting theorem and explaining how it works. then, we'll walk you through some practical examples of problems that can be solved using this. Second shifting property if $\mathcal {l} \left\ { f (t) \right\} = f (s)$, and $g (t) = \begin {cases} f (t a) & t \gt a \\ 0 & t \lt a \end {cases}$ then, $\mathcal {l} \left\ { g (t) \right\} = e^ { as} f (s)$. Is it a typo in the question or how does one go about solving this? i'm not looking for a solution, just some insight into how to go about dealing with the difference in shifts issue. We have seen how the laplace transform can be used to solve linear differential equations. familiar functions that arise in solutions to differential equations are e a t cos b t and . e a t sin b t the first shifting theorem will show how their transforms are related to those of cos b t and sin b t by shifting the variable s in . Learn how to apply both the first and second shift theorems to solve complex laplace transform problems with ease. sharpen your skills and boost your confidence in tackling a wide variety of laplace transform problems through the video’s step by step examples.

Solved Use The Second Shifting Theorem To Determine Chegg Second shifting property if $\mathcal {l} \left\ { f (t) \right\} = f (s)$, and $g (t) = \begin {cases} f (t a) & t \gt a \\ 0 & t \lt a \end {cases}$ then, $\mathcal {l} \left\ { g (t) \right\} = e^ { as} f (s)$. Is it a typo in the question or how does one go about solving this? i'm not looking for a solution, just some insight into how to go about dealing with the difference in shifts issue. We have seen how the laplace transform can be used to solve linear differential equations. familiar functions that arise in solutions to differential equations are e a t cos b t and . e a t sin b t the first shifting theorem will show how their transforms are related to those of cos b t and sin b t by shifting the variable s in . Learn how to apply both the first and second shift theorems to solve complex laplace transform problems with ease. sharpen your skills and boost your confidence in tackling a wide variety of laplace transform problems through the video’s step by step examples.

Solved The Second Shifting Theorem Replacing G By G 1 T Chegg We have seen how the laplace transform can be used to solve linear differential equations. familiar functions that arise in solutions to differential equations are e a t cos b t and . e a t sin b t the first shifting theorem will show how their transforms are related to those of cos b t and sin b t by shifting the variable s in . Learn how to apply both the first and second shift theorems to solve complex laplace transform problems with ease. sharpen your skills and boost your confidence in tackling a wide variety of laplace transform problems through the video’s step by step examples.

Immerse Yourself in Art, Culture, and Creativity: Celebrate the beauty of artistic expression with our How To Use Second Shifting Theorem For Solving Problems resources. From art forms to cultural insights, we'll ignite your imagination and deepen your appreciation for the diverse tapestry of human creativity.

How to use second shifting theorem for solving problems?

How to use second shifting theorem for solving problems?

How to use second shifting theorem for solving problems? Laplace Transform: Second Shifting Theorem Differential Equations Laplace Second Shifting Theorem 10.7 LaPlace Transforms Second Shifting Theorem BRCC Math 2904 The Second Translation Theorem for Laplace Transforms LAPLACE TRANSFORM (SECOND SHIFT THEOREM) Laplace transforms / differential equations Beyond Brute Force Unlocking Calculus with Focused and Diffuse Thinking Video Laplace Transform | Second Shifting Theorem | Concept & Example by GP Sir Second shifting theorem of Laplace transforms Laplace Transform. Second Translation Theorem. Laplace Transform - Second Shifting Theorem Laplace Transforms – Second Shift Theorem and Worked Examples 💪 Laplace Transform for Second Order Differential Equations (Forced Harmonic), Second Shifting Theorem Casio scientific calculator fx-991ES fx-100AU PLUS 2nd edition self-test function "shift-7-on" Table of Laplace transform Second shifting theorem: Laplace transforms Laplace transform, 1st and 2nd shifting theorem tutorial Second shifting theorem: Laplace transforms

Conclusion

Delving deeply into the topic, one can see that content provides valuable awareness pertaining to How To Use Second Shifting Theorem For Solving Problems. Throughout the content, the writer demonstrates a wealth of knowledge related to the field. Crucially, the examination of important characteristics stands out as a crucial point. The narrative skillfully examines how these factors influence each other to establish a thorough framework of How To Use Second Shifting Theorem For Solving Problems.

Moreover, the write-up is remarkable in deconstructing complex concepts in an digestible manner. This accessibility makes the content useful across different knowledge levels. The analyst further enriches the exploration by integrating relevant samples and actual implementations that situate the conceptual frameworks.

An additional feature that distinguishes this content is the thorough investigation of different viewpoints related to How To Use Second Shifting Theorem For Solving Problems. By exploring these multiple standpoints, the piece provides a impartial view of the matter. The thoroughness with which the writer treats the matter is highly praiseworthy and establishes a benchmark for related articles in this area.

To conclude, this post not only teaches the consumer about How To Use Second Shifting Theorem For Solving Problems, but also prompts more investigation into this captivating subject. For those who are just starting out or a veteran, you will find useful content in this detailed article. Thank you sincerely for taking the time to this detailed piece. If you have any questions, please feel free to reach out with our contact form. I am keen on your comments. In addition, you will find some relevant pieces of content that might be valuable and enhancing to this exploration. Hope you find them interesting!