How To Find The Inverse Of A Complex Number

Complex Numbers With Inverse Solution Pdf Complex Number How to find the inverse of a complex number if you enjoyed this video please consider liking, sharing, and subscribing .more. This article deals with this concept of additive inverse in good detail and also the method of finding additive inverse for each type of number such as integers, rational numbers, real numbers, complex numbers, etc. as well as other mathematical structures such as matrices.

1 6 Inverse Trigonometric And Inverse Hyperbolic Functions Of Complex I recently attempted to show that the multiplicative inverse for complex numbers exists and expressed it in complex form, as follows: suppose $z = a bi$ is a non zero complex number. To find the opposite of a complex number \ ( z \), simply reverse the signs of both its real and imaginary components. let's take a complex number \ ( z \): $$ z = 2 3i $$ its opposite has the same magnitude for both the real and imaginary parts, but with reversed signs: $$ z = 2 3i $$. Here you will learn how to find the reciprocal of a complex number with examples. let’s begin – how to find the reciprocal of a complex number the reciprocal is also called multiplicative inverse. let z = a ib be a non zero complex number. then \ (1\over z\) = \ (1\over a ib\) multiply numerator and denominator by conjugate of denominator,. Multiplicative inferse of a complex number explained with an interactive example.
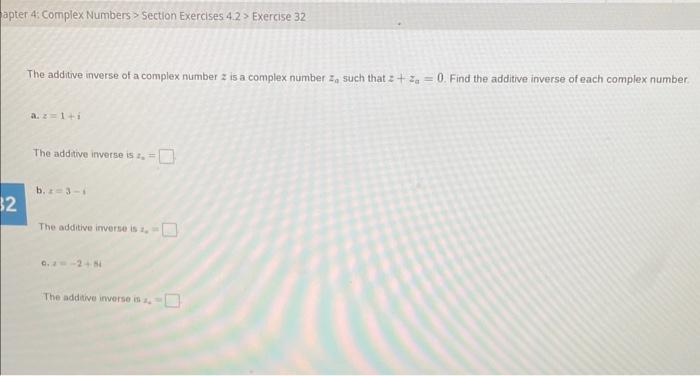
Solved The Additive Inverse Of A Complex Number Z Is A Chegg Here you will learn how to find the reciprocal of a complex number with examples. let’s begin – how to find the reciprocal of a complex number the reciprocal is also called multiplicative inverse. let z = a ib be a non zero complex number. then \ (1\over z\) = \ (1\over a ib\) multiply numerator and denominator by conjugate of denominator,. Multiplicative inferse of a complex number explained with an interactive example. Calculate modulus, conjugate, inverse, polar form and square root of any complex number with this step by step calculator. What is the inverse of a complex number? every non zero complex number z = x iy z=x iy has a "reciprocal" friend called the multiplicative inverse (or just inverse), which we write as z^ { 1} z−1 or 1 z 1 z. Inverse of a complex number. if z is a non zero complex number and z = x yi, the (multiplicative) inverse of z, denoted by z −1 or 1 z, is when z is written in polar form, so that z = reiθ = r (cos θ i sin θ), where r ≠ 0, the inverse of z is (1 r) e −iθ = (1 r) (cos θ− i sin θ). The inverse of a complex number is simply the reciprocal of the number, which is the fraction of 1 over the complex number. but usually it’s good practice for this fraction to be rationalized, which is where we again make use of the complex conjugate.

Find The Multiplicative Inverse Of The Complex Number I Maths Glow Calculate modulus, conjugate, inverse, polar form and square root of any complex number with this step by step calculator. What is the inverse of a complex number? every non zero complex number z = x iy z=x iy has a "reciprocal" friend called the multiplicative inverse (or just inverse), which we write as z^ { 1} z−1 or 1 z 1 z. Inverse of a complex number. if z is a non zero complex number and z = x yi, the (multiplicative) inverse of z, denoted by z −1 or 1 z, is when z is written in polar form, so that z = reiθ = r (cos θ i sin θ), where r ≠ 0, the inverse of z is (1 r) e −iθ = (1 r) (cos θ− i sin θ). The inverse of a complex number is simply the reciprocal of the number, which is the fraction of 1 over the complex number. but usually it’s good practice for this fraction to be rationalized, which is where we again make use of the complex conjugate.
Comments are closed.