How To Determine If A Sequence Converges The Friendly Statistician
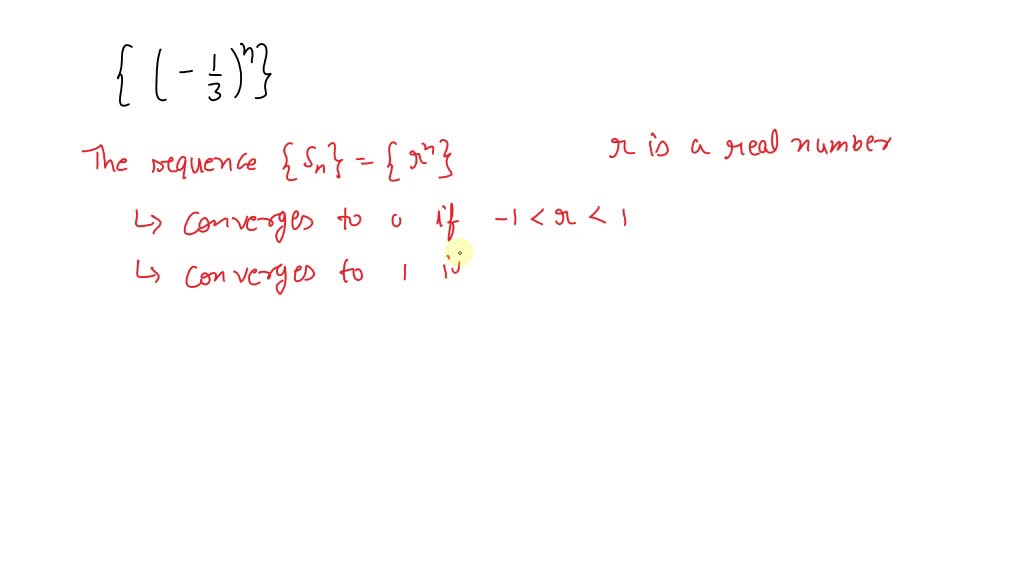
Solved Determine Whether The Given Sequence Converges If The Sequence In this informative video, we’ll break down the concept of convergence in sequences. understanding how a sequence approaches a specific limit is essential in mathematics and statistics . One thing you are often asked to do is to prove that an estimator (appropriately scaled) converges in distribution, and you are often asked to determine that limiting distribution. in this post, i list some strategies you can use for that. note: this list is not exhaustive.

Solved Determine Whether The Given Sequence Converges If The Sequence When random variables converge on a single number, they may not settle exactly that number, but they come very, very close. in notation, x (x n → x) tells us that a sequence of random variables (x n) converges to the value x. If we say that a sequence converges, it means that the limit of the sequence exists as n tends toward infinity. if the limit of the sequence as doesn’t exist, we say that the sequence diverges. a sequence always either converges or diverges, there is no other option. The basic question is this: what can we say about the limiting behavior of a sequence of random variablesx1;x2;x3;:::? since statistics is all about gathering data, we will naturally be interested in what happens as we gather more and more data, hence our interest in this question. There are four types of convergence that we will discuss in this section: almost sure convergence. these are all different kinds of convergence. a sequence might converge in one sense but not another. some of these convergence types are ''stronger'' than others and some are ''weaker.''.

Solved Determine Whether The Given Sequence Converges If The Sequence The basic question is this: what can we say about the limiting behavior of a sequence of random variablesx1;x2;x3;:::? since statistics is all about gathering data, we will naturally be interested in what happens as we gather more and more data, hence our interest in this question. There are four types of convergence that we will discuss in this section: almost sure convergence. these are all different kinds of convergence. a sequence might converge in one sense but not another. some of these convergence types are ''stronger'' than others and some are ''weaker.''. In this informative video, we will introduce you to the concept of a convergent sequence and its significance in the realm of statistics, particularly in the analysis of categorical data and. In this section, we will develop the theoretical background to study the convergence of a sequence of random variables in more detail. in particular, we will define different types of convergence. As the number of terms increases, the sequence approaches the limit or horizontal asymptote; λ tells you the rate at which that happens. if positive constants λ and α exist for the above limit, then the sequence converges to p of order of α at rate λ. Let x1 xn x 1 x n be a sequence of random variables that converges in probability to a constant a. assume that p(xi> 0) = 1 p (x i> 0) = 1 for all i. verify that the sequences defined by yi = a xi y i = a x i converge in probability. i will give the solution to this problem below and then point out where i am having trouble.

Solved Determine Whether The Given Sequence Converges If The Sequence In this informative video, we will introduce you to the concept of a convergent sequence and its significance in the realm of statistics, particularly in the analysis of categorical data and. In this section, we will develop the theoretical background to study the convergence of a sequence of random variables in more detail. in particular, we will define different types of convergence. As the number of terms increases, the sequence approaches the limit or horizontal asymptote; λ tells you the rate at which that happens. if positive constants λ and α exist for the above limit, then the sequence converges to p of order of α at rate λ. Let x1 xn x 1 x n be a sequence of random variables that converges in probability to a constant a. assume that p(xi> 0) = 1 p (x i> 0) = 1 for all i. verify that the sequences defined by yi = a xi y i = a x i converge in probability. i will give the solution to this problem below and then point out where i am having trouble.

Solved 3 Determine If The Following Sequences Converge Or Chegg As the number of terms increases, the sequence approaches the limit or horizontal asymptote; λ tells you the rate at which that happens. if positive constants λ and α exist for the above limit, then the sequence converges to p of order of α at rate λ. Let x1 xn x 1 x n be a sequence of random variables that converges in probability to a constant a. assume that p(xi> 0) = 1 p (x i> 0) = 1 for all i. verify that the sequences defined by yi = a xi y i = a x i converge in probability. i will give the solution to this problem below and then point out where i am having trouble.
Comments are closed.