Gaussian Process Regression Gaussian Processes For Regression A Quick
Gaussian Process Regression Gaussian Processes For Regression A Quick In mathematics, a gaussian function, often simply referred to as a gaussian, is a function of the base form and with parametric extension for arbitrary real constants a, b and non zero c. In one dimension, the gaussian function is the probability density function of the normal distribution, f (x)=1 (sigmasqrt (2pi))e^ ( (x mu)^2 (2sigma^2)), (1) sometimes also called the frequency curve.
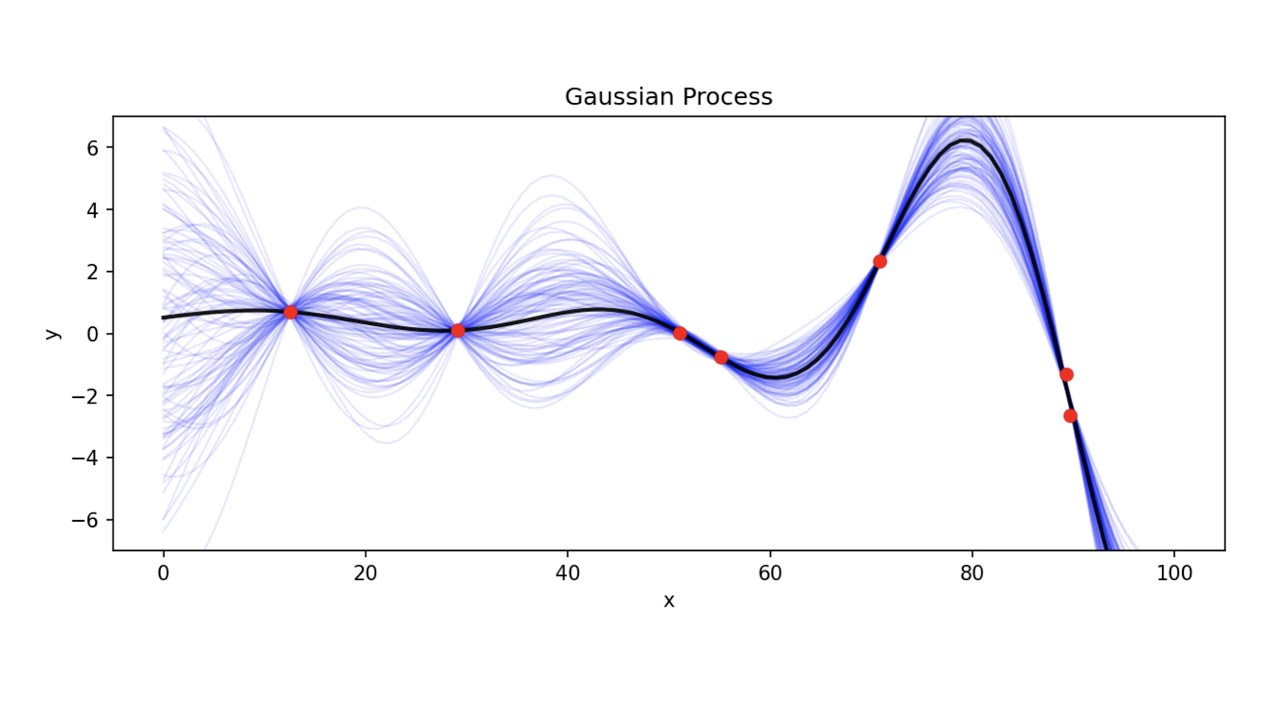
Gaussian Processes Regression Basic Introductory Example 53 Off Gaussian is a registered trademark of gaussian, inc. this website has been tested with the current versions of firefox, chrome, safari and microsoft edge as of august 2023. older versions are not supported for all pages. Gaussian distribution a gaussian distribution, also referred to as a normal distribution, is a type of continuous probability distribution that is symmetrical about its mean; most observations cluster around the mean, and the further away an observation is from the mean, the lower its probability of occurring. like other probability distributions, the gaussian distribution describes how the. In mathematics, a gaussian function (named after carl friedrich gauss) is a function of the form: for some real constants a > 0, b, c > 0, and e ≈ 2.718281828 (euler's number). the graph of a gaussian is a characteristic symmetric "bell shape curve" that quickly falls off towards plus minus infinity. The gaussian distribution shown is normalized so that the sum over all values of x gives a probability of 1. the nature of the gaussian gives a probability of 0.683 of being within one standard deviation of the mean.
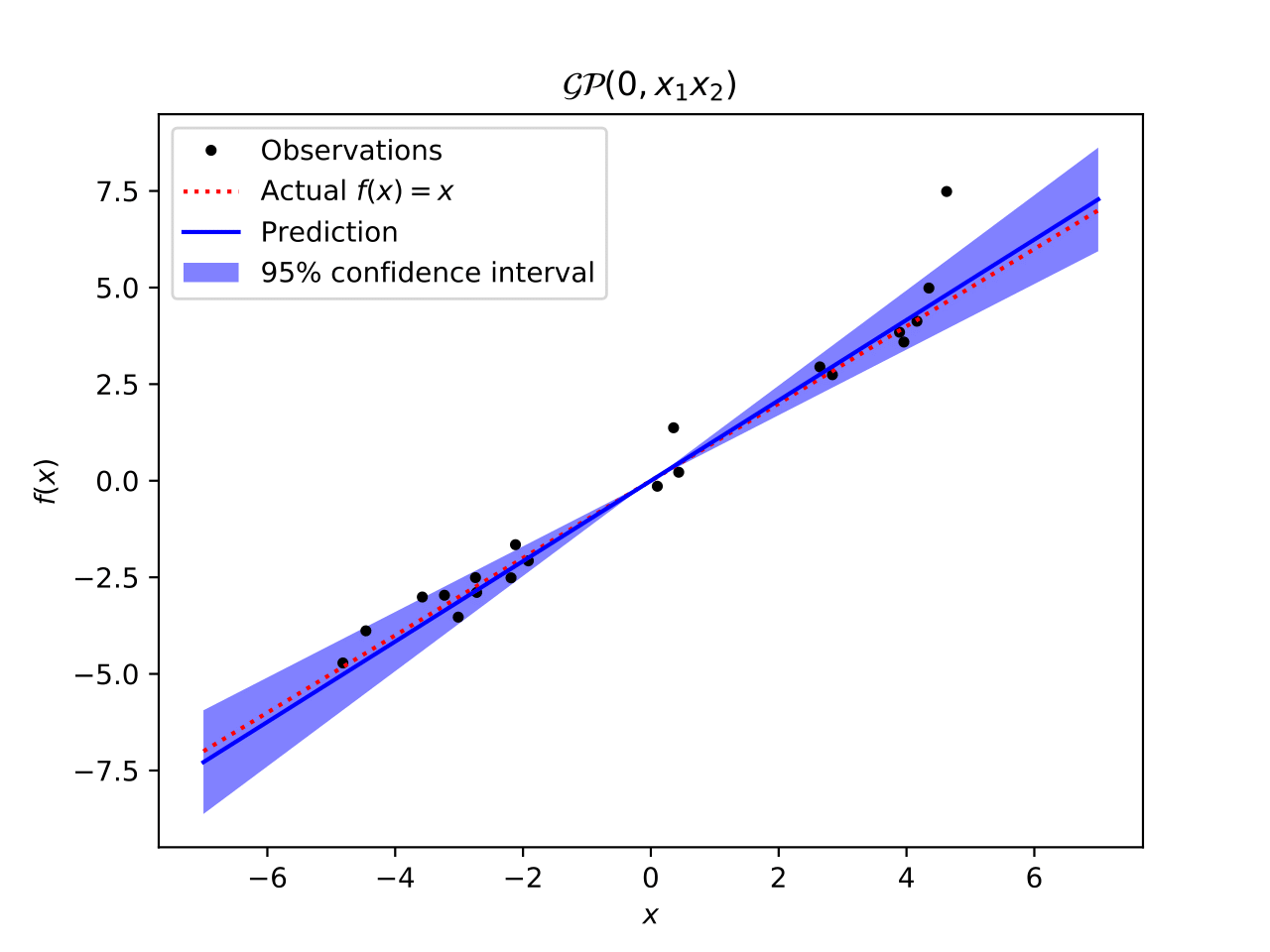
Gaussian Process Regression Edison Weik My Blog In mathematics, a gaussian function (named after carl friedrich gauss) is a function of the form: for some real constants a > 0, b, c > 0, and e ≈ 2.718281828 (euler's number). the graph of a gaussian is a characteristic symmetric "bell shape curve" that quickly falls off towards plus minus infinity. The gaussian distribution shown is normalized so that the sum over all values of x gives a probability of 1. the nature of the gaussian gives a probability of 0.683 of being within one standard deviation of the mean. % = var = % other names: gaussian random variable mean variance ~ ( , ) 0.5. In probability theory and statistics, a normal distribution or gaussian distribution is a type of continuous probability distribution for a real valued random variable. In mathematics, a gaussian function, often simply referred to as a gaussian, is a function of the base form and with parametric extension for arbitrary real constants, and non zero . Gaussian 16 is the latest in the gaussian series of programs. it provides state of the art capabilities for electronic structure modeling. gaussian 16 is licensed for a wide variety of computer systems.

Quick Start To Gaussian Process Regression Geeksforgeeks % = var = % other names: gaussian random variable mean variance ~ ( , ) 0.5. In probability theory and statistics, a normal distribution or gaussian distribution is a type of continuous probability distribution for a real valued random variable. In mathematics, a gaussian function, often simply referred to as a gaussian, is a function of the base form and with parametric extension for arbitrary real constants, and non zero . Gaussian 16 is the latest in the gaussian series of programs. it provides state of the art capabilities for electronic structure modeling. gaussian 16 is licensed for a wide variety of computer systems.

Gaussian Process Regression In mathematics, a gaussian function, often simply referred to as a gaussian, is a function of the base form and with parametric extension for arbitrary real constants, and non zero . Gaussian 16 is the latest in the gaussian series of programs. it provides state of the art capabilities for electronic structure modeling. gaussian 16 is licensed for a wide variety of computer systems.
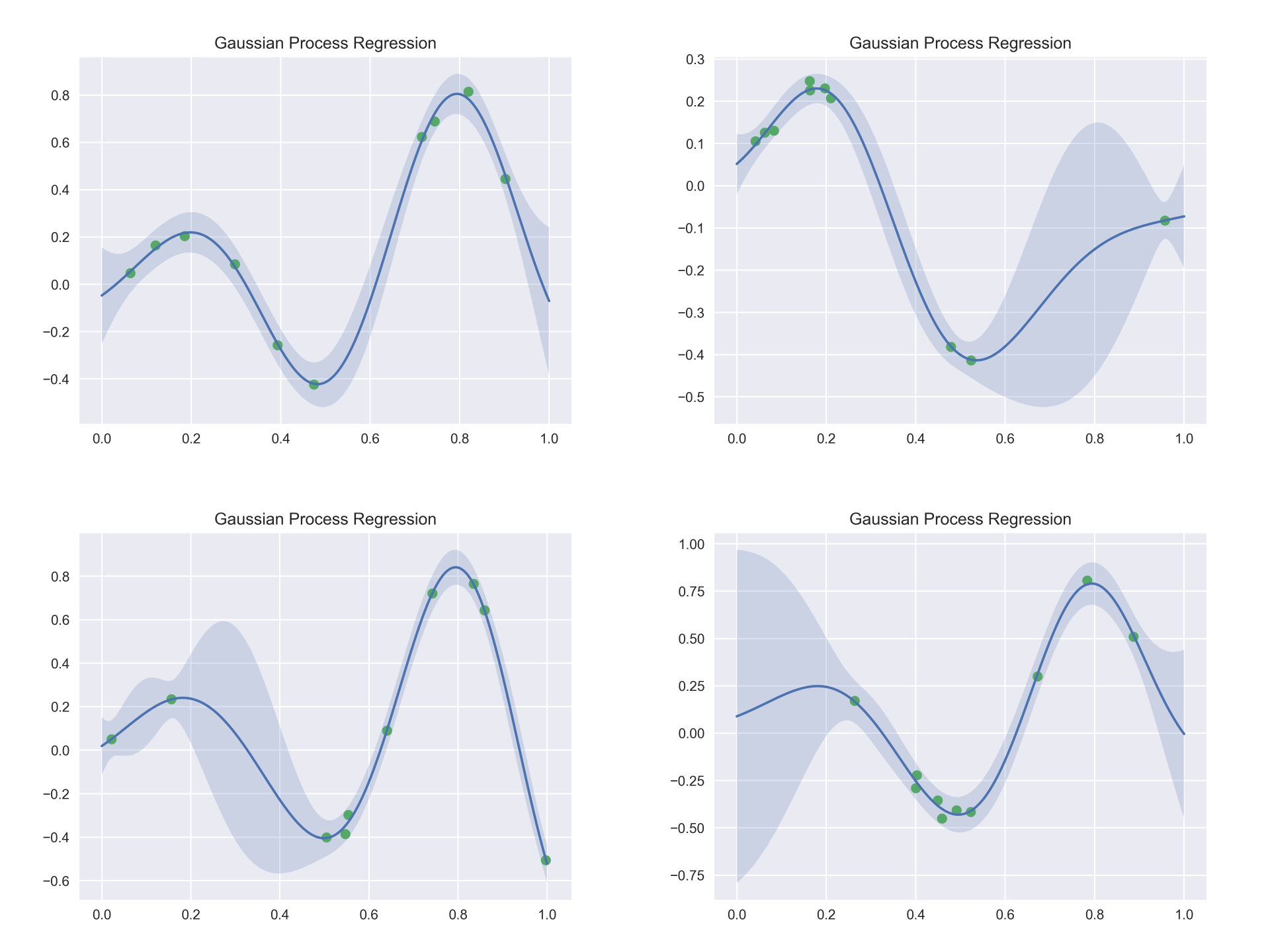
Gaussian Process Regression Mathtoolbox
Comments are closed.