Functions And Graphs Checking If An Equation Represents A Function

Which Equation Represents The Graphed Function Scope Revealer Sal determines if y is a function of x from looking at an equation. created by sal khan. If the function is graphically represented where the input is the x x coordinate and output is the y y coordinate, we can use the vertical line test to determine if it is a function. if any vertical line drawn can cross the graph at a maximum of one point, then the graph is a function.
Solved Here Is The Graph That Represents A Function Which Equation In the last section we learned how to determine if a relation is a function. the relations we looked at were expressed as a set of ordered pairs, a mapping or an equation. we will now look at how to tell if a graph is that of a function. If a vertical line touches the graph of an equation more than once, then the graph does not represent a function. in this case, we would say the graph "fails the vertical line test.". When i’m looking at equations and trying to determine if they represent a function, i consider the definition of a function. a function pairs each input value from the domain with exactly one output value in the range. In this video i demonstrate an example of how to check whether an equation of a graph represents a function.
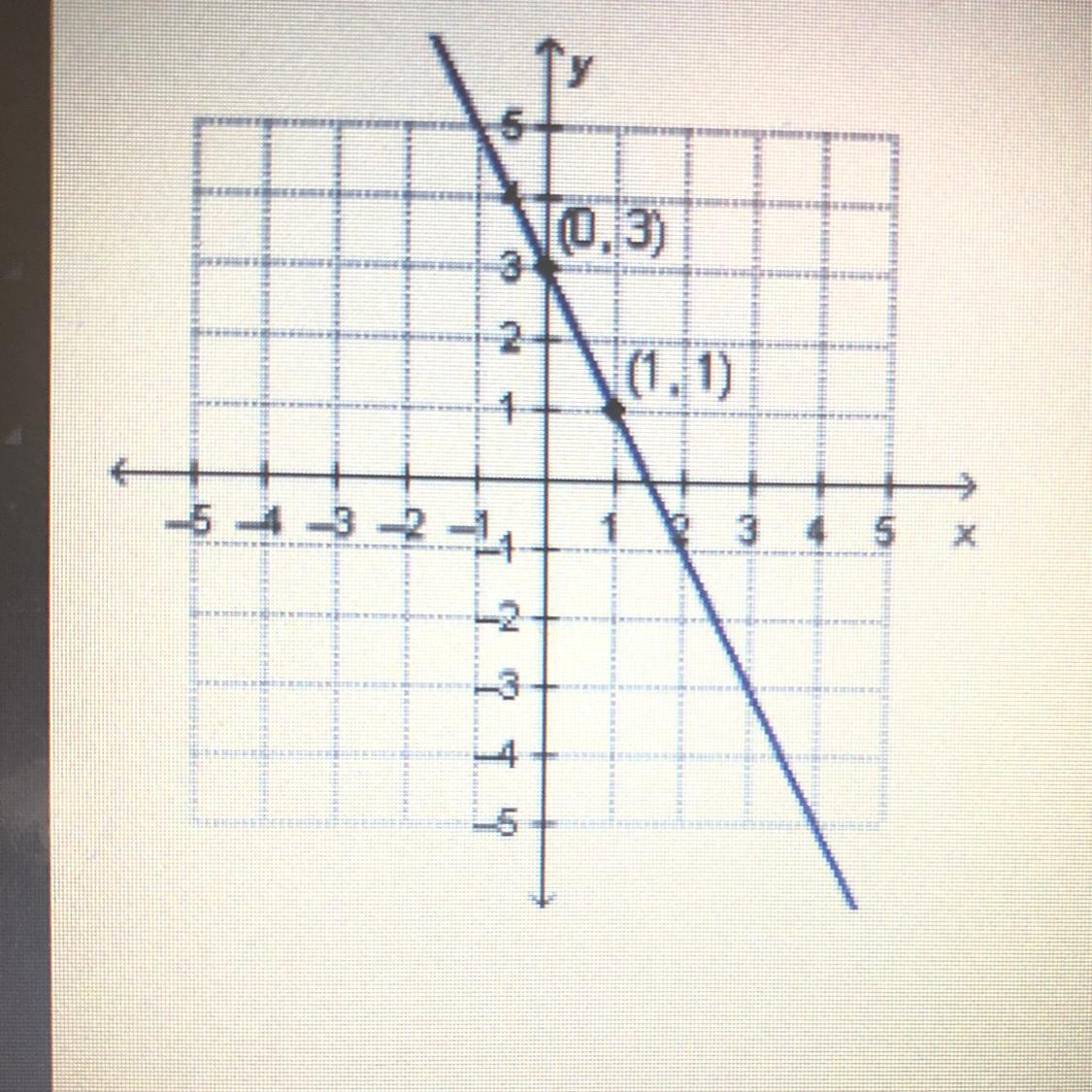
Which Equation Represents The Graphed Function When i’m looking at equations and trying to determine if they represent a function, i consider the definition of a function. a function pairs each input value from the domain with exactly one output value in the range. In this video i demonstrate an example of how to check whether an equation of a graph represents a function. You will work through 3 examples of determining which graph represents a function and a function with direct variation from four possible choices and how to easily find a correct answer using the vertical line test. How to: given a graph, use the vertical line test to determine if the graph represents a function. inspect the graph to see if any vertical line drawn would intersect the curve more than once. if there is any such line, the graph does not represent a function. First, we will start discussing graphing equations by introducing the cartesian (or rectangular) coordinates system and illustrating use of the coordinate system to graph lines and circles. we will also formally define a function and discuss graph functions and combining functions. we will also discuss inverse functions.
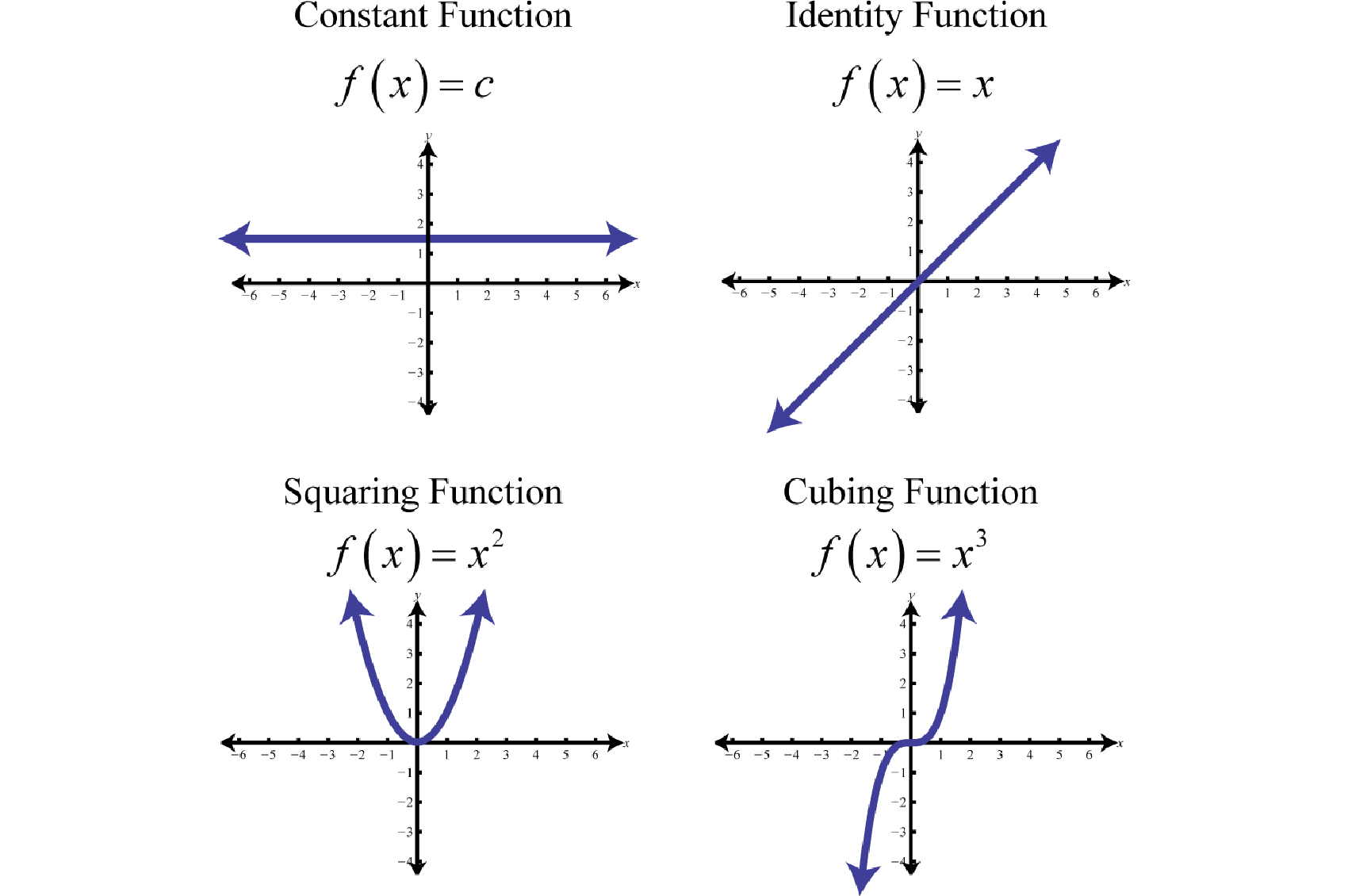
Basic Functions Graphs You will work through 3 examples of determining which graph represents a function and a function with direct variation from four possible choices and how to easily find a correct answer using the vertical line test. How to: given a graph, use the vertical line test to determine if the graph represents a function. inspect the graph to see if any vertical line drawn would intersect the curve more than once. if there is any such line, the graph does not represent a function. First, we will start discussing graphing equations by introducing the cartesian (or rectangular) coordinates system and illustrating use of the coordinate system to graph lines and circles. we will also formally define a function and discuss graph functions and combining functions. we will also discuss inverse functions.
Choose The Correct Equation For The Function Whose Graph Is Shown First, we will start discussing graphing equations by introducing the cartesian (or rectangular) coordinates system and illustrating use of the coordinate system to graph lines and circles. we will also formally define a function and discuss graph functions and combining functions. we will also discuss inverse functions.
Comments are closed.