Floating Point Rounding Error In Computer By Himashaamarasingha Medium

Floating Point Rounding Error In Computer By Himashaamarasingha Medium Here, we’ll go over a step by step conversion process for converting from an ieee 754 standard binary representation to a decimal floating point number. Explanation of the reasons for rounding errors in floating point math, and of rounding modes.

Rounding Errors Lab Pdf Rounding Integer Computer Science I am aware that floating point arithmetic has precision problems. i usually overcome them by switching to a fixed decimal representation of the number, or simply by neglecting the error. Now i'm trying to solve this puzzle and i think i'm getting some rounding floating point error. so i'm finally going to figure out the basics of floating point error. In computer there is a standard called ieee 754. this is the standard computer use to represent the floating point size of each section defined according to the precision. When you manually convert a floating point number to binary, the result may differ from the binary representation produced by a computer. this is called the floating point rounding.

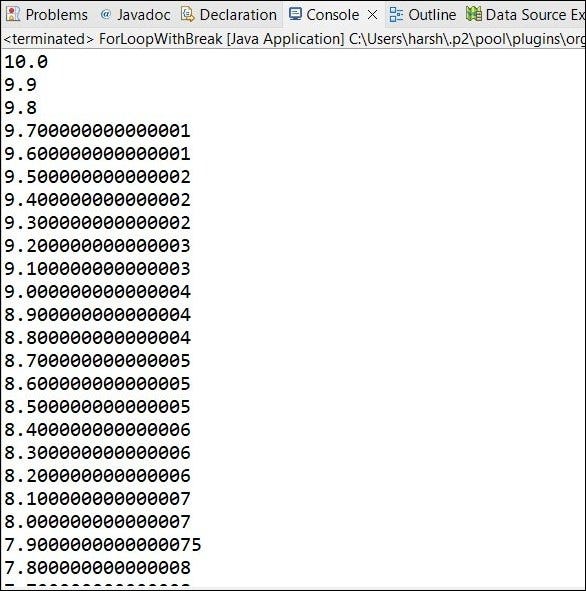
Floating Point Error 2 Floating Point Rounding Error In Computer By In computer there is a standard called ieee 754. this is the standard computer use to represent the floating point size of each section defined according to the precision. When you manually convert a floating point number to binary, the result may differ from the binary representation produced by a computer. this is called the floating point rounding. If you have no idea about fundamentals and how computer deals with the floating point numbers, you may have to deal with some hard situations that occurs by these even without your knowledge . The same non commutativity principle applies to most if not all other floating point operations. compilers are not allowed to produce non spec compliant results, so this annoying nuance disables some potential optimizations that involve rearranging operands in arithmetic. Therefore, the result of a floating point calculation must often be rounded off to fit into a finite representation. this rounding error is a characteristic feature of floating point. The document discusses the limitations of computer floating point arithmetic and the resulting round off errors due to the finite representation of real numbers.