Finding Local Maxima And Minima By Differentiation

6 Differentiation Minima And Maxima Pdf Calculus Mathematical Well if we are looking at the graph of a function, differentiation makes it super easy to find where any local maxima and minima occur. this act in itself has many applications, but. In this article, we will discuss the introduction, definition, and important terminology of local maxima and minima and its meaning. we will also understand the different methods to calculate the local maxima and minima in mathematics and calculus.
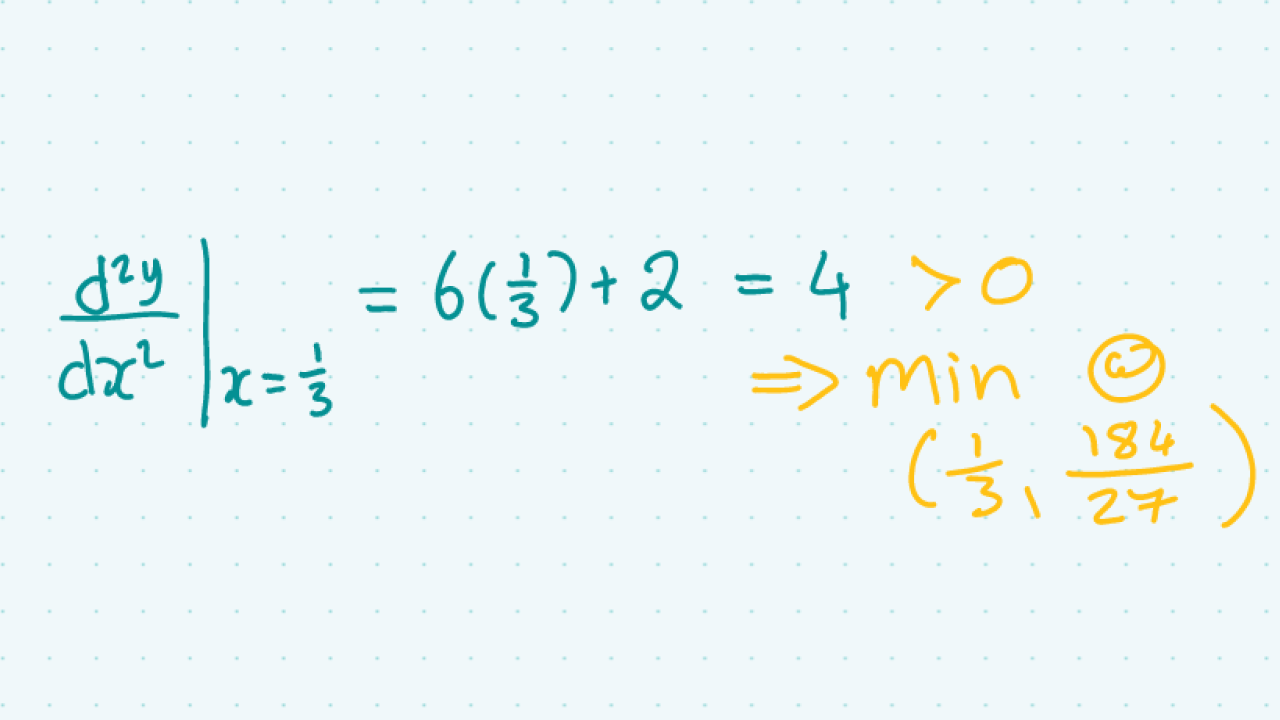
Finding Local Maxima And Minima Turning Points Studyclix Apply the four cases of the test to determine whether each critical point is a local maximum, local minimum, or saddle point, or whether the theorem is inconclusive. Thus, to find local maximum and minimum points, we need only consider those points at which both partial derivatives are 0. as in the single variable case, it is possible for the derivatives to be 0 at a point that is neither a maximum or a minimum, so we need to test these points further. First we need to formalize what we mean. definition.f(c) is the absolute maximum value of f if f(c) f(x) for all x. f(c) is the absolute minimum value of f if f(c) f(x) for all x. f(c) is a local maximum if f(c) f(x) for all x near c. f(c) is a local minimum if f(c) f(x) for all x near c. Local maximum or local minimum first we need to choose an interval: the local maximum is the point where the height of the function at "a" is greater than (or equal to) the height anywhere else in that interval.

Application Of Differentiation Pdf Maxima And Minima Functions First we need to formalize what we mean. definition.f(c) is the absolute maximum value of f if f(c) f(x) for all x. f(c) is the absolute minimum value of f if f(c) f(x) for all x. f(c) is a local maximum if f(c) f(x) for all x near c. f(c) is a local minimum if f(c) f(x) for all x near c. Local maximum or local minimum first we need to choose an interval: the local maximum is the point where the height of the function at "a" is greater than (or equal to) the height anywhere else in that interval. If the function goes from increasing to decreasing, then that point is a local maximum. if the function goes from decreasing to increasing, then that point is a local minimum. To find all local maxima and minima of a function in a given interval, there are three primary methods: the first derivative test, the second derivative test, and the higher order derivative test. Differentiation can be used to find the coordinates of these stationary points and also can help to distinguish between the local maximum and minimum points. the increasing sections of f (x) is shown in red, and decreasing section is shown in black. This video explain how to find the local maxima and minima coordinated on a curve using differentiation.
Comments are closed.