Equivalent Graphs Graph Theory

Graph Theory Pdf An “invariant” is a graph property that remains the same for all graphs in any isomorphism class. thus, if you can find an invariant that is different for two graphs, you know that these graphs must not be isomorphic. Graphs are fully defined by their vertices and edges. the exact position of each vertex and edge doesn’t matter—only which nodes are connected to each other. as such,two equivalent graphs can look very diferent.
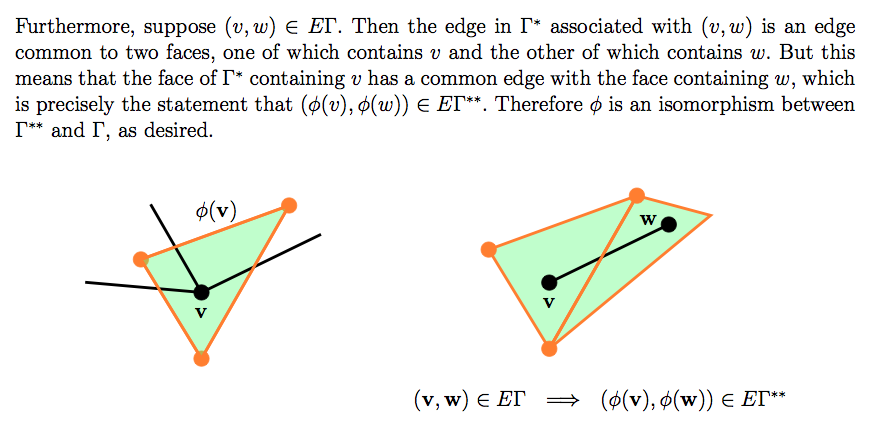
Not Only Truth But Supreme Beauty Graph Theory Graph Theory Is The This video goes over the most basic graph theory concepts. we cover vertices, edges, loops, and equivalent graphs, along with going over some common misconc. When you think about a graph, you seems to think about the abstract pattern that is common to all isomorphic graphs. mathematicians do the same, but must distinguish between them formally, else 1 become 2. Since an equivalence relation partitions a set into a disjoint union of equivalence classes (theorem 18.3.8), the graph of an equivalence relation will be disconnected, with each connected component representing a specific equivalence class. In summary, equivalent graphs are useful in many mathematical and computational applications, such as graph theory, network analysis, and algorithm design, where it is important to recognize and exploit similarities or symmetries between graphs to solve problems efficiently.

Studying Logic Proofsareart Graph Theory Graph Theory Is The Since an equivalence relation partitions a set into a disjoint union of equivalence classes (theorem 18.3.8), the graph of an equivalence relation will be disconnected, with each connected component representing a specific equivalence class. In summary, equivalent graphs are useful in many mathematical and computational applications, such as graph theory, network analysis, and algorithm design, where it is important to recognize and exploit similarities or symmetries between graphs to solve problems efficiently. The 15 dominating nonunique graphs on five or fewer vertices are illustrated above. a graph that does not share a domination polynomial with any other nonisomorphic graph is said to be a dominating unique graph (akbari et al. 2010). Two nonisomorphic graphs g and h are said to be matching equivalent if and only if g and h have the same matching polynomials. in this paper, some families matching equivalent graphs are constructed. Graph equivalence is an important concept in graph theory, indicating that two graphs are structurally the same, even if they appear different on the surface. two graphs are considered equivalent if you can map vertices from one graph to another in such a way that preserves connectivity. As long as two graphs indicate the same pattern of connections, like graph a and graph f, they are considered to be equal, or in graph theory terms, isomorphic.
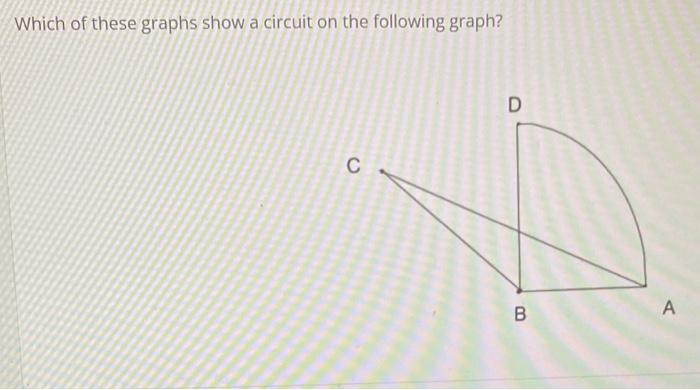
Which Of These Graphs Is Equivalent To The Graph Chegg The 15 dominating nonunique graphs on five or fewer vertices are illustrated above. a graph that does not share a domination polynomial with any other nonisomorphic graph is said to be a dominating unique graph (akbari et al. 2010). Two nonisomorphic graphs g and h are said to be matching equivalent if and only if g and h have the same matching polynomials. in this paper, some families matching equivalent graphs are constructed. Graph equivalence is an important concept in graph theory, indicating that two graphs are structurally the same, even if they appear different on the surface. two graphs are considered equivalent if you can map vertices from one graph to another in such a way that preserves connectivity. As long as two graphs indicate the same pattern of connections, like graph a and graph f, they are considered to be equal, or in graph theory terms, isomorphic.
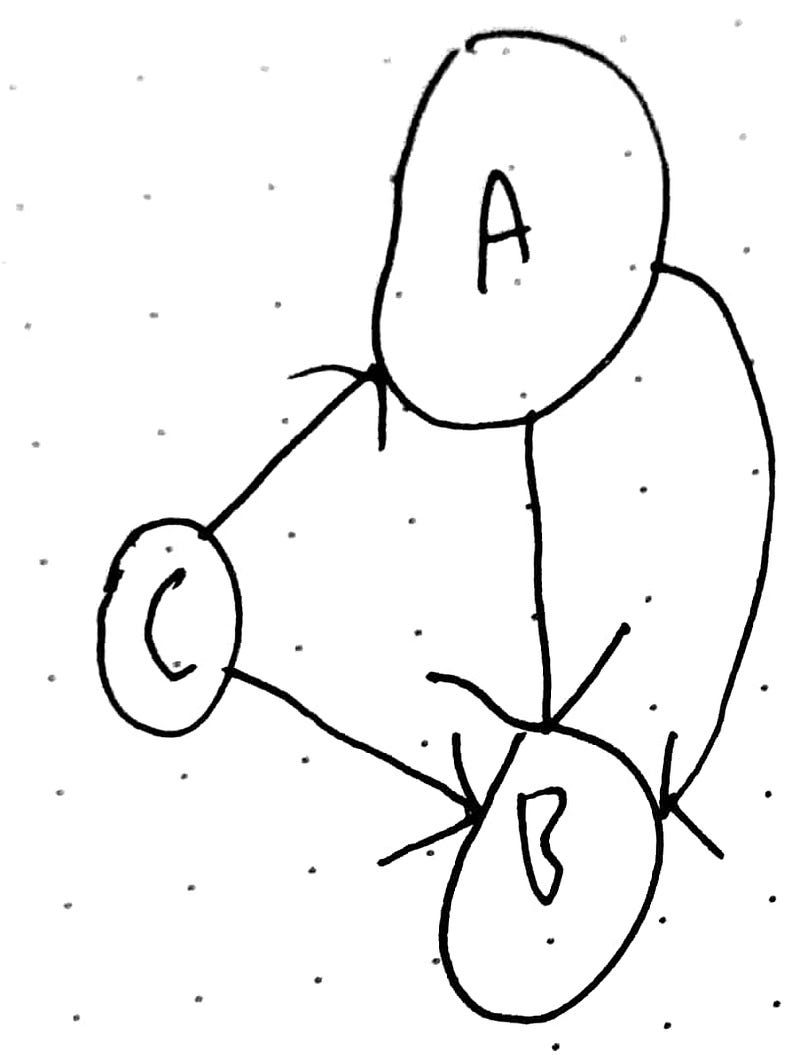
Graph Theory Graph equivalence is an important concept in graph theory, indicating that two graphs are structurally the same, even if they appear different on the surface. two graphs are considered equivalent if you can map vertices from one graph to another in such a way that preserves connectivity. As long as two graphs indicate the same pattern of connections, like graph a and graph f, they are considered to be equal, or in graph theory terms, isomorphic.
Comments are closed.