Division Algorithm Mathsquad

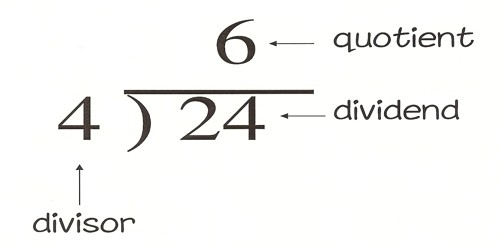
Division Algorithm Assignment Point As with other operations, there are many ways of performing division (not just many perspectives). you are likely aware of the fact that we can directly model (if the numbers are fairly small and usually integers), repeatedly subtract the divisor, or use long division. Division algorithm for the above division : problem 2 : divide 258 by 9, list out dividend, divisor, quotient, remainder and write division algorithm. solution : as we have seen in problem 1, if we divide 258 by 9 using long division, we get. dividend = 258. divisor = 9. quotient = 28. remainder = 6. division algorithm for the above division is.

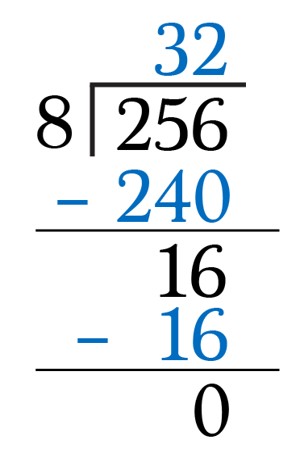
Division Algorithm Assignment Point The division algorithm the division algorithm for integers says the following: given two positive integers a and b, with b 6= 0, there exists unique integers q and r such that a = qb r where 0 r < jbj. The division algorithm in this capsule we will discuss the process of developing a division algorithm. If you are super confident in your ability to answer these questions on using the division algorithm and equivalent fractions then you’re ready to move onto activity 2. for more information (including answers to each question) just click on an image and you’ll be connected to the skill’s web page. Prove using the division algorithm that every integer is either even or odd, but never both. definition \ (\pageindex {2}\) by the parity of an integer we mean whether it is even or odd. prove \ (n\) and \ (n^2\) always have the same parity. that is, \ (n\) is even if and only if \ (n^2\) is even.

Division Algorithm Profe Social If you are super confident in your ability to answer these questions on using the division algorithm and equivalent fractions then you’re ready to move onto activity 2. for more information (including answers to each question) just click on an image and you’ll be connected to the skill’s web page. Prove using the division algorithm that every integer is either even or odd, but never both. definition \ (\pageindex {2}\) by the parity of an integer we mean whether it is even or odd. prove \ (n\) and \ (n^2\) always have the same parity. that is, \ (n\) is even if and only if \ (n^2\) is even. The reason i want to go through the proof of the division algorithm is not because i think that students are, or should be, skeptical, but because the proof illustrates some important ways of thinking. There exists a unique pair of integers q and r, such that n = q · d r and 0 ≤ r < d. q = qcnt(n, d) is the quotient, r = rem(n, d) is the remainder. i’d call them “integer division” and “mod” and sometimes i’ll write r = n%d. examples: qcnt(2716, 10) = 271. since 2716 = 271 · 10 6 rem(2716, 10) = 6. same reason. rem(−11, 7) = 3. Division algorithm says dividend = divisor x quotient remainder. this is used to find whether the division performed is correct or not. the division algorithm can also be applied for polynomials. it is used to find one of the division terms.

Division Algorithm Mathsquad The reason i want to go through the proof of the division algorithm is not because i think that students are, or should be, skeptical, but because the proof illustrates some important ways of thinking. There exists a unique pair of integers q and r, such that n = q · d r and 0 ≤ r < d. q = qcnt(n, d) is the quotient, r = rem(n, d) is the remainder. i’d call them “integer division” and “mod” and sometimes i’ll write r = n%d. examples: qcnt(2716, 10) = 271. since 2716 = 271 · 10 6 rem(2716, 10) = 6. same reason. rem(−11, 7) = 3. Division algorithm says dividend = divisor x quotient remainder. this is used to find whether the division performed is correct or not. the division algorithm can also be applied for polynomials. it is used to find one of the division terms.

Division Algorithm Mathsquad Division algorithm says dividend = divisor x quotient remainder. this is used to find whether the division performed is correct or not. the division algorithm can also be applied for polynomials. it is used to find one of the division terms.

Division Algorithm Mathsquad