Discrete Fourier Transform Dft 1

Mathematics Of The Discrete Fourier Transform Dft With Audio Today we introduced a new fourier representation for dt signals: the discrete fourier transform (dft). the dft has a number of features that make it particularly convenient. As you may recall from fourier analysis, the fourier transform of a convolution is the product of the transforms; the same property holds for the discrete fourier transform.
Discrete Fourier Transform Dft Discrete Fourier Transform Research 1 The discrete fourier transform this chapter builds on the definition and discussion of the dtft in chapter 66. the objective here is to define a numerical fourier transform called the discrete fourier transform (or dft) that results from taking frequency samples of the dtft. − cfs represents a continuous periodic signal using an infinite number of complex exponentials, whereas − dfs represents a discrete periodic signal using a finite number of complex exponentials. How can we compute the dtft? the dtft has a big problem: it requires an in nite length summation, therefore you can't compute it on a computer. the dft solves this problem by assuming a nite length signal. Like continuous time signal fourier transform, discrete time fourier transform can be used to represent a discrete sequence into its equivalent frequency domain representation and lti discrete time system and develop various computational algorithms.

Fft Dan Dft Pdf How can we compute the dtft? the dtft has a big problem: it requires an in nite length summation, therefore you can't compute it on a computer. the dft solves this problem by assuming a nite length signal. Like continuous time signal fourier transform, discrete time fourier transform can be used to represent a discrete sequence into its equivalent frequency domain representation and lti discrete time system and develop various computational algorithms. The discrete fourier transform is just a multiplication of a matrix to the given sequence of signal. naively computing the matrix multiplication requires o(n2) operations. 9.4 discrete fourier transform (dft) the discrete time fourier transform, dtft, can be derived also in the process of numerical evaluation of the integral that defines the fourier transform. consider the basic definition of the fourier transform and approximate it by an infinite sum obtained by performing sampling (discretiza. The convolution property of the dft is somewhat di erent from the convolution property for the continuous time fourier transform, so it deserves special attention. For example, the dft is used in state of the art algorithms for multiplying polynomials and large integers together; instead of working with polynomial multiplication directly, it turns out to be faster to compute the dft of the polynomial functions and convert the problem of multiplying polynomials to an analogous problem involving their dfts.

Discrete Fourier Transform Dft Numxl The discrete fourier transform is just a multiplication of a matrix to the given sequence of signal. naively computing the matrix multiplication requires o(n2) operations. 9.4 discrete fourier transform (dft) the discrete time fourier transform, dtft, can be derived also in the process of numerical evaluation of the integral that defines the fourier transform. consider the basic definition of the fourier transform and approximate it by an infinite sum obtained by performing sampling (discretiza. The convolution property of the dft is somewhat di erent from the convolution property for the continuous time fourier transform, so it deserves special attention. For example, the dft is used in state of the art algorithms for multiplying polynomials and large integers together; instead of working with polynomial multiplication directly, it turns out to be faster to compute the dft of the polynomial functions and convert the problem of multiplying polynomials to an analogous problem involving their dfts.

Discrete Fourier Transform Dft Dr Malaya Kumar Hota Prof Sense The convolution property of the dft is somewhat di erent from the convolution property for the continuous time fourier transform, so it deserves special attention. For example, the dft is used in state of the art algorithms for multiplying polynomials and large integers together; instead of working with polynomial multiplication directly, it turns out to be faster to compute the dft of the polynomial functions and convert the problem of multiplying polynomials to an analogous problem involving their dfts.
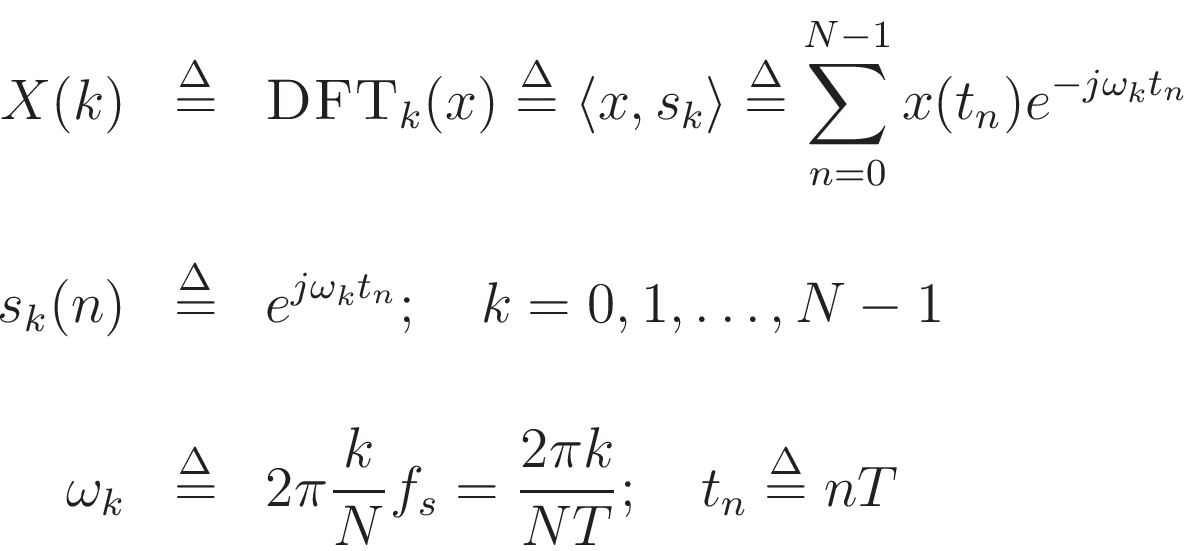
The Discrete Fourier Transform
Comments are closed.