Differential Equations Solution Using Numerical Methods Methods Of

Numerical Methods For Ordinary Differential Equations Pdf Numerical Numerical methods for ordinary differential equations are methods used to find numerical approximations to the solutions of ordinary differential equations (odes). It is in these complex systems where computer simulations and numerical methods are useful. the techniques for solving differential equations based on numerical approximations were developed before programmable computers existed.
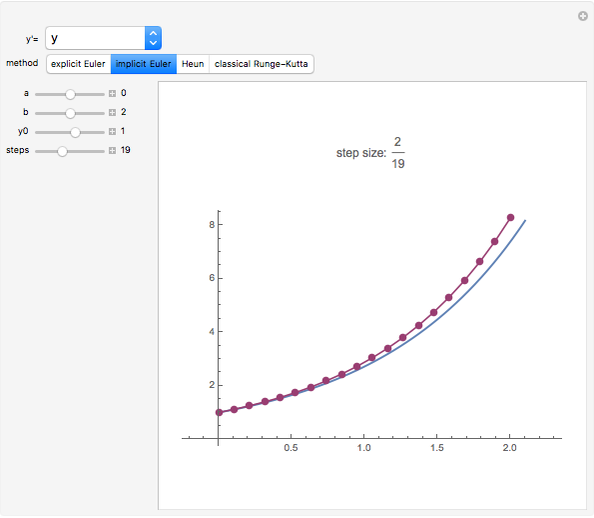
Numerical Methods For Differential Equations Wolfram Demonstrations The first order differential equation and the given initial value constitute a first order initial value problem given as: = ( , ) ; 0 = 0, whose numerical solution may be given using any of the following methodologies:. Numerical methods in differential equations are techniques used to approximate the solutions of differential equations when an exact, analytical solution is difficult or impossible to obtain. Explore numerical solutions to differential equations with mathmultiverse’s guide, covering euler’s method, runge kutta, detailed examples, and applications in physics and engineering. 5. homogeneity a differential equation is homogeneous if and only if u(t) ≡ 0 is a solution. example: = sin(t)u(t) t2 is a first order, linea.

Numerical Methods For Solving Ordinary Differential Equations Pdf Explore numerical solutions to differential equations with mathmultiverse’s guide, covering euler’s method, runge kutta, detailed examples, and applications in physics and engineering. 5. homogeneity a differential equation is homogeneous if and only if u(t) ≡ 0 is a solution. example: = sin(t)u(t) t2 is a first order, linea. Numerical solutions of differential equations are essential methods used to find approximate solutions for equations that describe various physical phenomena in science and engineering. Learn the numerical methods used to solve differential equations, including euler's method, runge kutta methods, and finite difference methods. In this detailed guide, we will explore various numerical methods for solving differential equations. we will discuss the theory behind these methods in depth as well as provide examples and visual illustrations to enhance understanding. Second order differential equations in which first order derivatives do not appear are found so frequently in applied problems, particularly those arising from the law of motion, that special methods have been devised for their solution.

Numerical Methods For Differential Equations Homework 1 Numerical solutions of differential equations are essential methods used to find approximate solutions for equations that describe various physical phenomena in science and engineering. Learn the numerical methods used to solve differential equations, including euler's method, runge kutta methods, and finite difference methods. In this detailed guide, we will explore various numerical methods for solving differential equations. we will discuss the theory behind these methods in depth as well as provide examples and visual illustrations to enhance understanding. Second order differential equations in which first order derivatives do not appear are found so frequently in applied problems, particularly those arising from the law of motion, that special methods have been devised for their solution.

Numerical Solution Of Ordinary Differential Equations Gtu Cvnm Ppt In this detailed guide, we will explore various numerical methods for solving differential equations. we will discuss the theory behind these methods in depth as well as provide examples and visual illustrations to enhance understanding. Second order differential equations in which first order derivatives do not appear are found so frequently in applied problems, particularly those arising from the law of motion, that special methods have been devised for their solution.

Solved 2 Numerical Methods For Solving Ordinary Chegg
Comments are closed.