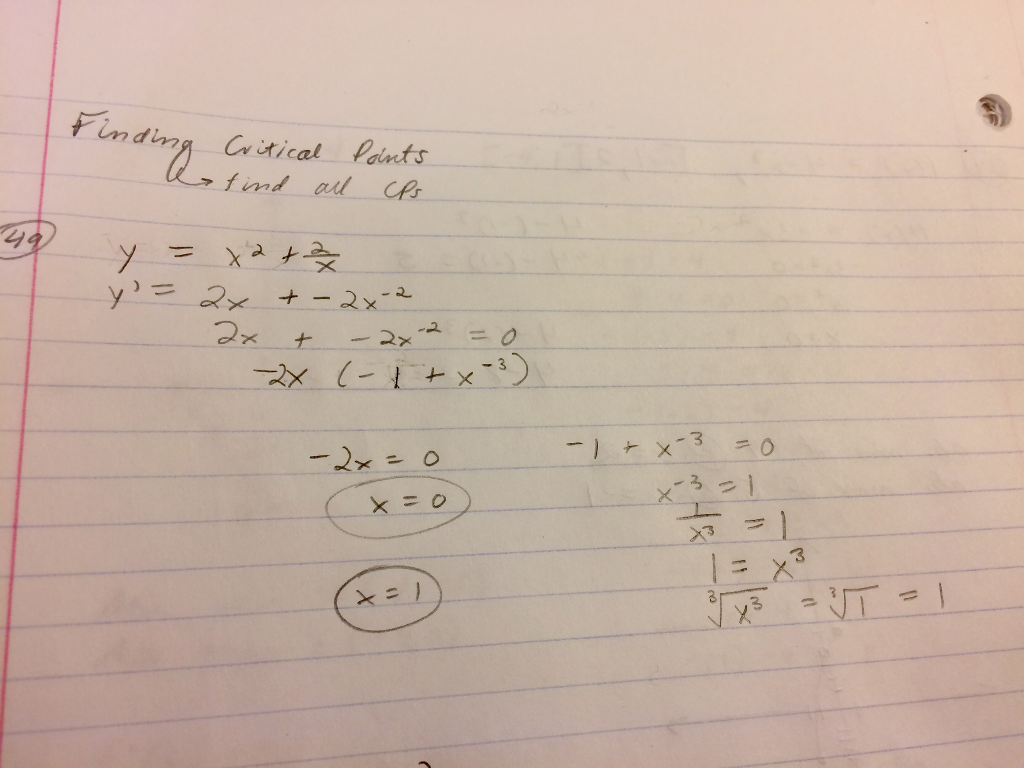
Solved Finding Critical Points Absolute Max And Min Not Chegg In this video, i share with you steps for using derivatives to find the values of p and q in function f (x) = x^2 px q such that f (1) = 5 is an extremum o. Imagine you are standing on a local maximum of the graph of a two variable function z = f(x; y). this means that in every direction you travel, you will lose elevation.
Solved Find Critical Points And Extreme Values Max Min Of Chegg These two graphs illustrate why a function over a bounded interval may fail to have an absolute maximum and or absolute minimum. before looking at how to find absolute extrema, let’s examine the related concept of local extrema. this idea is useful in determining where absolute extrema occur. Based on the information given, classify each of the following points as a local maximum, local minimum, saddle point, not a critical point, or not enough information to classify. Example 6: find any critical points and classify them as local min max on second derivative test. If an absolute extremum does not occur at an endpoint, however, it must occur at an interior point, in which case the absolute extremum is a local extremum. therefore, by fermat’s theorem, the point [latex]c [ latex] at which the local extremum occurs must be a critical point.
Local Min Max Critical Points Worksheet Studocu Example 6: find any critical points and classify them as local min max on second derivative test. If an absolute extremum does not occur at an endpoint, however, it must occur at an interior point, in which case the absolute extremum is a local extremum. therefore, by fermat’s theorem, the point [latex]c [ latex] at which the local extremum occurs must be a critical point. Find the critical points for each function. use the first derivative test to determine whether the critical point is a local maximum, local minimum, or neither. The question that now confronts us is: given a set of critical points, how can we decide if each is a local minimum, local maximum, or neither? the answer lies in the second derivative test. Trema an. itical conditio. the (firs. we f0 . must poi. e that t. orem. in. in the h. us how t. point a. xample. t is one, then it nec. sarily has zer. , then canot achie. ion valu. s . points wh. terior point o. the do. arante. above . s of (2) e. al. in . he sense that . s zero or. global m. min. exam. and m. . we fo. e endpoi. ) = 8t t4. In this ultimate guide, we provide clear methods for finding local maxima and minima using critical points, derivative tests, graphical insights, and practical examples.
Comments are closed.