Converting Units With Conversion Factors Dimensional Analysis

Converting Units With Conversion Factors Dimensional 52 Off Describe how to use dimensional analysis to carry out unit conversions for a given property and computations involving two or more properties. convert between the three main temperature units: fahrenheit, celsius, and kelvin. The main idea in dimensional analysis is to create a conversion ratio (unit factor) which has the units you want in the numerator and the units you already have in the denominator. it may be necessary to multiply by more than one conversion ratio in more difficult problems.
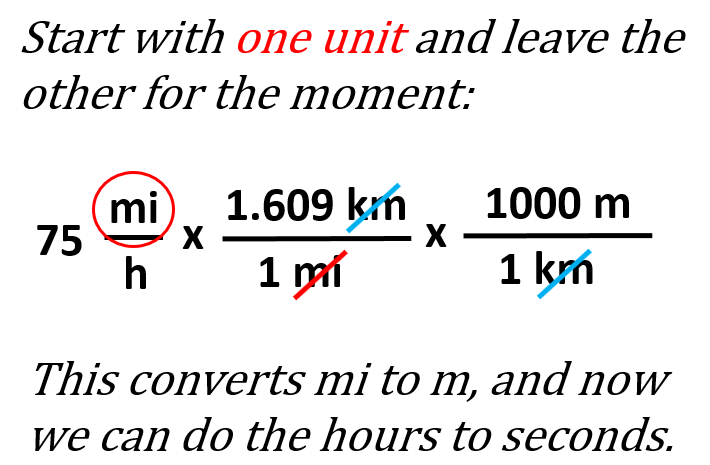
Converting Units With Conversion Factors Dimensional 50 Off Identify the conversion factor needed to get to the desired unit. put your units in such a way as to cancel what you have and get the unit you want. below, you will find some of the most common prefixes used in unit conversions. the unit we are given are milligrams and we need to cover them to grams. This metric system review video tutorial provides an overview review of how to convert from one unit to another using a technique called dimensional analysis or the factor label method . Dimensional analysis can be used to solve any conversion problem and allows problems to be easily checked for possible errors. this handout focuses on the most common conversions: metric, chemical, and multi step. Discover how dimensional analysis and conversion factors can simplify complex calculations. learn about derived units and how they relate to speed and distance in real world scenarios.

Converting Units With Conversion Factors Metric System Review Dimensional analysis can be used to solve any conversion problem and allows problems to be easily checked for possible errors. this handout focuses on the most common conversions: metric, chemical, and multi step. Discover how dimensional analysis and conversion factors can simplify complex calculations. learn about derived units and how they relate to speed and distance in real world scenarios. In this section, we will learn how to use conversion factors and dimensional analysis to convert between different units of mass and weight, such as kilograms, pounds, newtons, and ounces. Multi unit conversions using dimensional analysis dimensional analysis is useful when converting betw. en multiple systems of measurement at the same time. example 1: given the speed of a car on a highway is 1. h, how fast is the car travelling in miles min? km h since we are considering both length and time, we need. on fact. Dimensional analysis uses conversion factors to change the unit in an amount into an equivalent quantity expressed with a different unit. for example, a conversion factor could be used to convert 3.55 meters to centimeters. To perform dimensional analysis, you first identify the given quantity and its units. then, set up the conversion factor (s) as ratios representing the relationship between different units. next, multiply by the conversion factor to ensure the units cancel out, leaving you with the desired unit.

Units Dimensional Analysis And Conversion Factors Summary Learncheme In this section, we will learn how to use conversion factors and dimensional analysis to convert between different units of mass and weight, such as kilograms, pounds, newtons, and ounces. Multi unit conversions using dimensional analysis dimensional analysis is useful when converting betw. en multiple systems of measurement at the same time. example 1: given the speed of a car on a highway is 1. h, how fast is the car travelling in miles min? km h since we are considering both length and time, we need. on fact. Dimensional analysis uses conversion factors to change the unit in an amount into an equivalent quantity expressed with a different unit. for example, a conversion factor could be used to convert 3.55 meters to centimeters. To perform dimensional analysis, you first identify the given quantity and its units. then, set up the conversion factor (s) as ratios representing the relationship between different units. next, multiply by the conversion factor to ensure the units cancel out, leaving you with the desired unit.

Converting Units With Conversion Factors Dimensional Analysis Dimensional analysis uses conversion factors to change the unit in an amount into an equivalent quantity expressed with a different unit. for example, a conversion factor could be used to convert 3.55 meters to centimeters. To perform dimensional analysis, you first identify the given quantity and its units. then, set up the conversion factor (s) as ratios representing the relationship between different units. next, multiply by the conversion factor to ensure the units cancel out, leaving you with the desired unit.
Comments are closed.