Continuity Basic Introduction Point Infinite Jump Discontinuity Removable Nonremovable

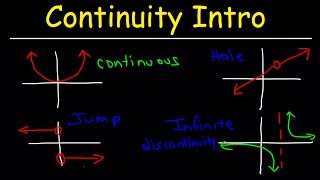
Continuity Basic Introduction Point Infinite Jump Discontinuity The jump continuity, as its name suggests, occurs when the curve jumps from one place to the other place at the point where it has jump continuity. in other words, the left hand sided limit and right handed sided limits at the point with jump discontinuity are not equal. Intuitively, a removable discontinuity is a discontinuity for which there is a hole in the graph, a jump discontinuity is a noninfinite discontinuity for which the sections of the function do not meet up, and an infinite discontinuity is a discontinuity located at a vertical asymptote.

Solved 3 1 1 Point Continuous Jump Discontinuity Removable There are two types of discontinuities: removable and non removable. then there are two types of non removable discontinuities: jump or infinite discontinuities. For a function to be continuous at a point from a given side, we need the following three conditions: the function is defined at the point. the function has a limit from that side at that point. the one sided limit equals the value of the function at the point. This calculus video tutorial provides a basic introduction into to continuity. it explains the difference between a continuous function and a discontinuous one. Unlike removable discontinuities, a function with a non removable discontinuity cannot be re defined in such a way that the function becomes continuous. two types of non removable discontinuities include jump discontinuities and infinite discontinuities:.

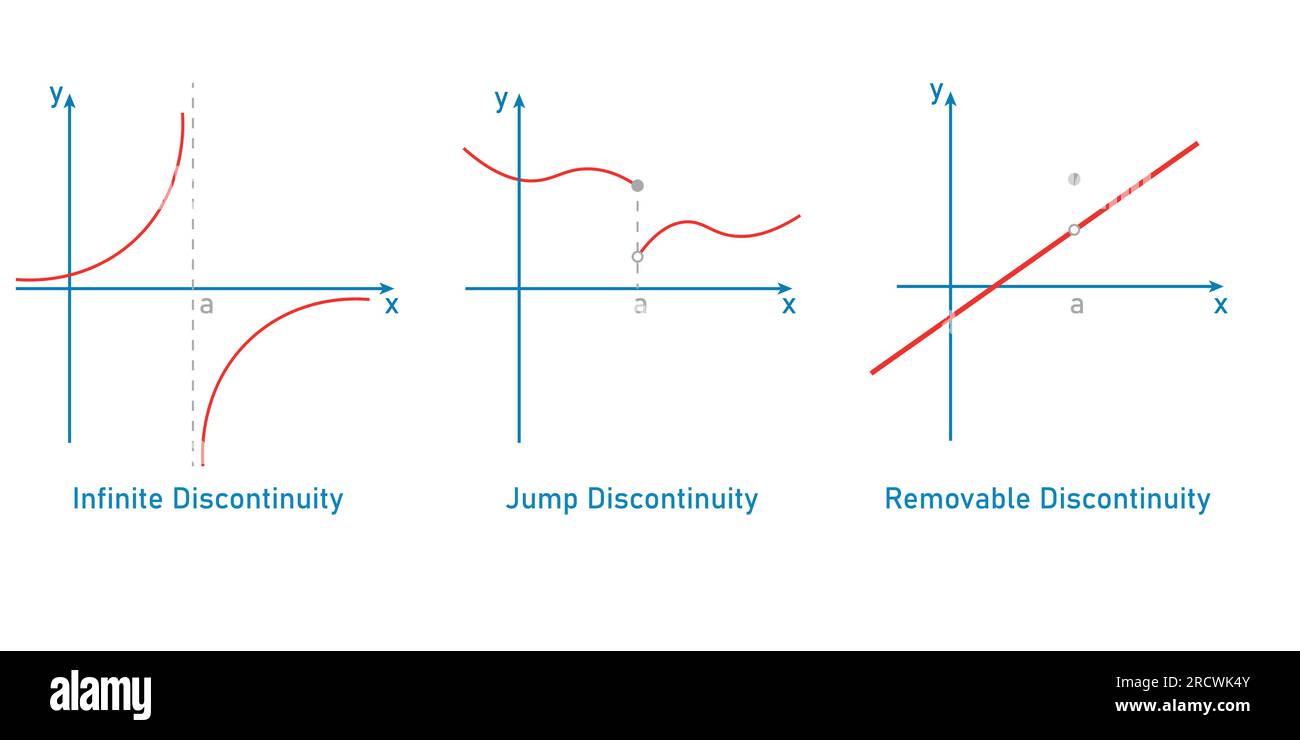
Types Of Discontinuity Of A Function Infinite Jump And Removable This calculus video tutorial provides a basic introduction into to continuity. it explains the difference between a continuous function and a discontinuous one. Unlike removable discontinuities, a function with a non removable discontinuity cannot be re defined in such a way that the function becomes continuous. two types of non removable discontinuities include jump discontinuities and infinite discontinuities:. Around t = 0, we need to look at the limits from both sides. knowing the sign of t lets us simplify the absolute value operation, and the rest is just limit laws. since both limits exist but aren’t equal, we have a jump discontinuity. everywhere except t=0 and t=1, f (t) is continuous. At a particular point we can classify three types of discontinuities. each . infinite. (ii) jump. discontinuities. what type of discontinuity is illustrated by the graphs of as shown. illustrated. discontinuous. at each of these points, state the type of discontinuity . Intuitively, a removable discontinuity is a discontinuity for which there is a hole in the graph, a jump discontinuity is a noninfinite discontinuity for which the sections of the function do not meet up, and an infinite discontinuity is a discontinuity located at a vertical asymptote.