Computational Method To Solve The Partial Differential Equations Pdes

Computational Method To Solve The Partial Differential Equations Pdes This article provides a comprehensive examination of computational techniques for solving pdes, delving into discretization methods, numerical algorithms, and their applications across. This text aims at equipping the readerwith tools and skills forformulating solution methods for pdes and producing associated running code. successful problem solving by means of mathematical models in science and engineering often demands a synthesis of knowledge from several elds.

Computational Method To Solve The Partial Differential Equations Pd In this popular text for an numerical analysis course, the authors introduce several major methods of solving various partial differential equations (pdes) including elliptic, parabolic, and hyperbolic equations. For partial di erential equations (pdes), we need to know the initial values and extra information about the behaviour of the solution u(x; t) at the boundary of the spatial domain (i.e. at x = a and x = b in this example). The core of ai for pdes is the fusion of data and partial differential equations (pdes), which can solve almost any pdes. therefore, this article provides a comprehensive review of the research on ai for pdes, summarizing the existing algorithms and theories. This easy to read book introduces the basics of solving partial differential equations by means of finite difference methods. unlike many of the traditional academic works on the topic, this book was written for practitioners.

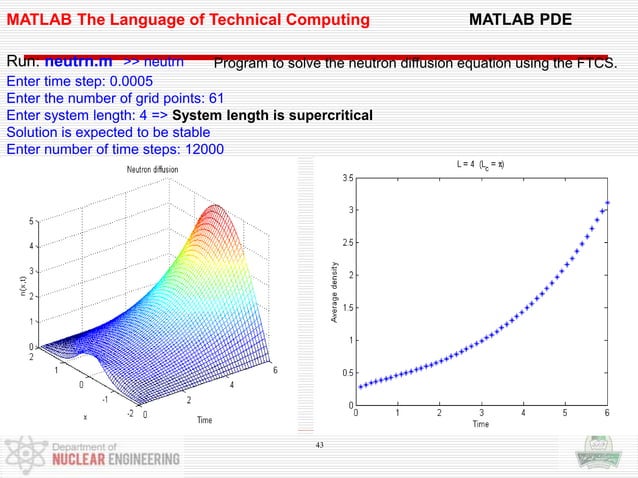
Computational Method To Solve The Partial Differential Equations Pdes The core of ai for pdes is the fusion of data and partial differential equations (pdes), which can solve almost any pdes. therefore, this article provides a comprehensive review of the research on ai for pdes, summarizing the existing algorithms and theories. This easy to read book introduces the basics of solving partial differential equations by means of finite difference methods. unlike many of the traditional academic works on the topic, this book was written for practitioners. To demonstrate the efficacy of our method, we apply the newly developed strategy to three different equations, achieving improved accuracy and reduced computational costs compared to previous approaches which incorporate the pretraining technique. Diferential equations (pdes) is essential in computational physics. over the past few decades, various qu. ntum based methods have been developed to formulate and solve pdes. solving. Deep learning has revolutionized the way we approach solving partial differential equations (pdes). by leveraging neural networks' ability to approximate complex functions, several methodologies have been developed to address the challenges posed by pdes. 1. We call the general solution of the pde (1.1), the family of functions u : Ω ⊂ rd r that has continuous partial derivatives up to (and including) order k and that satisfies (1.1). →. for any differentiable function f : r r.