Causal Discovery In Linear Structural Causal Models With Deterministic

By healtycares On Aug 25, 2025

Causal Discovery In Linear Structural Causal Models With Deterministic We derive a set of necessary and sufficient conditions for unique identifiability of the causal structure. to the best of our knowledge, this is the first work that gives identifiability results for causal discovery under both latent confounding and deterministic relationships. To the best of our knowledge, this is the first work that gives identifiability results for causal discovery under both latent confounding and deterministic relationships.

Causal Discovery In Linear Structural Causal Models With Deterministic Propagation scm demo code for "causal discovery in linear structural causal models with deterministic relations" by yuqin yang, mohamed nafea, amiremad ghassami and negar kiyavash, clear 2022. Summary: this paper considers the causal discovery problem in linear structural causal models, where the observed variables are of a deterministic function of other observed variables or latent confounders, but not with an exogenous source. We show that the independence between the error term and causes, together with appropriate structural constraints on the structural equation, makes it possible. next, we report some recent advances in causal discovery from time series. This paper focuses on a subclass of linear scms which do not have this property, i.e., models in which observed variables can be causally affected by any subset of the sources, and are allowed to be a deterministic function of other observed variables or latent confounders.

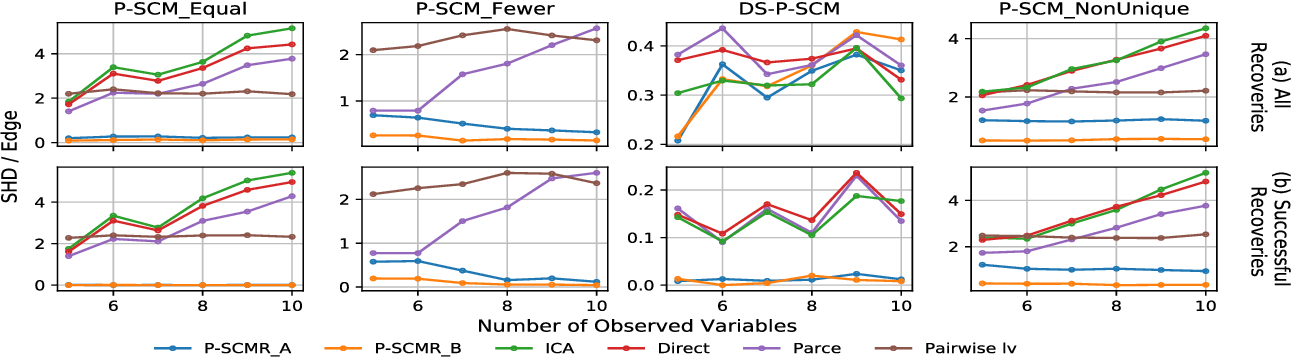
Causal Discovery In Linear Structural Causal Models With Deterministic We show that the independence between the error term and causes, together with appropriate structural constraints on the structural equation, makes it possible. next, we report some recent advances in causal discovery from time series. This paper focuses on a subclass of linear scms which do not have this property, i.e., models in which observed variables can be causally affected by any subset of the sources, and are allowed to be a deterministic function of other observed variables or latent confounders. Eliably infer cause effect relations from available data. the field of causal discovery seeks to address this challenge by clarifying when it is theo retically possible to infer a causal effect and by developing practical methods to estimate. Theorem 1:under faithfulness & source separability, a linear p scm is uniquely identifiable if and only if conditions 1 and 2 hold for every observed variable.*. We study the problem of causal discovery when the data generating model is a linear p scm, that is, to learn the directions and strengths of the causal influences among the observed variables, as well as the direct connections from the sources to the observed variables. We assume that the underlining pro cess or the measurement error free variables follows a linear, non guassian causal model, and show that the so called ordered group decomposition of the causal model, which con tains major causal information, is identifiable.

Welcome to our blog, a haven of knowledge and inspiration where Causal Discovery In Linear Structural Causal Models With Deterministic takes center stage. We believe that Causal Discovery In Linear Structural Causal Models With Deterministic is more than just a topic—it's a catalyst for growth, innovation, and transformation. Through our meticulously crafted articles, in-depth analysis, and thought-provoking discussions, we aim to provide you with a comprehensive understanding of Causal Discovery In Linear Structural Causal Models With Deterministic and its profound impact on the world around us.

[NeurIPS 2020] Causal Discovery in Physical Systems from Videos

[NeurIPS 2020] Causal Discovery in Physical Systems from Videos

[NeurIPS 2020] Causal Discovery in Physical Systems from Videos PGM 18Spring Lecture 13 updated: Causal Discovery Nicola Gnecco: Causal Discovery in Heavy-Tailed Models Causal Explanations of Structural Causal Models Talk at CIIG 8.2 Constraint-Based Casual Discovery For Non-Linear Structural Causal Models An Overview of Causal Discovery Causal Learning & Discovery Classical Strategies and Concepts in Causal Discovery Causal discovery from data: the problem with “unfaithful” structural models Classical Strategies and Concepts in Causal Discovery Structure Learning for Cyclic Linear Causal Models Tutorial on Causal Learning - Richard Scheines 4.7 - Structural Causal Models SCMs Lecture 08 - Causal Discovery and Inference July 24th 5 Beyond Structural Causal Models Causal Constraints Models Causality 3: Defining causality: Structural causal models (SCM) 6.S091 Lecture 1: Structural Causal Models Causal Discovery Elizabeth Silver — Causality and Causal Discovery 10 - Causal Discovery from Observational Data

Conclusion

Having examined the subject matter thoroughly, there is no doubt that the content presents informative awareness on Causal Discovery In Linear Structural Causal Models With Deterministic. From beginning to end, the blogger shows a wealth of knowledge in the field. Specifically, the part about critical factors stands out as a major point. The text comprehensively covers how these features complement one another to form a complete picture of Causal Discovery In Linear Structural Causal Models With Deterministic.

Further, the content is exceptional in clarifying complex concepts in an accessible manner. This simplicity makes the material valuable for both beginners and experts alike. The author further enhances the discussion by introducing related examples and concrete applications that provide context for the abstract ideas.

Another aspect that makes this post stand out is the detailed examination of multiple angles related to Causal Discovery In Linear Structural Causal Models With Deterministic. By analyzing these various perspectives, the content offers a balanced understanding of the theme. The comprehensiveness with which the content producer handles the subject is truly commendable and raises the bar for comparable publications in this field.

In summary, this content not only enlightens the consumer about Causal Discovery In Linear Structural Causal Models With Deterministic, but also encourages further exploration into this interesting field. Whether you are just starting out or an authority, you will find something of value in this thorough piece. Thank you for engaging with the article. If you would like to know more, please feel free to get in touch via the discussion forum. I am eager to hearing from you. For more information, here is several related articles that you will find useful and complementary to this discussion. Happy reading!