Calculate The Acceleration Of Block A And B In Cases Ab And C

Solved What Is The Acceleration Of Block C And Its Chegg A block of mass 5 kg is (i) pushed in case (a) and (ii) pulled in case (b), by a force f = 20 n, making an angle of 30∘ with the horizontal, as shown in the figures. Calculate the acceleration of block a and b in cases (a), (b), and (c ).
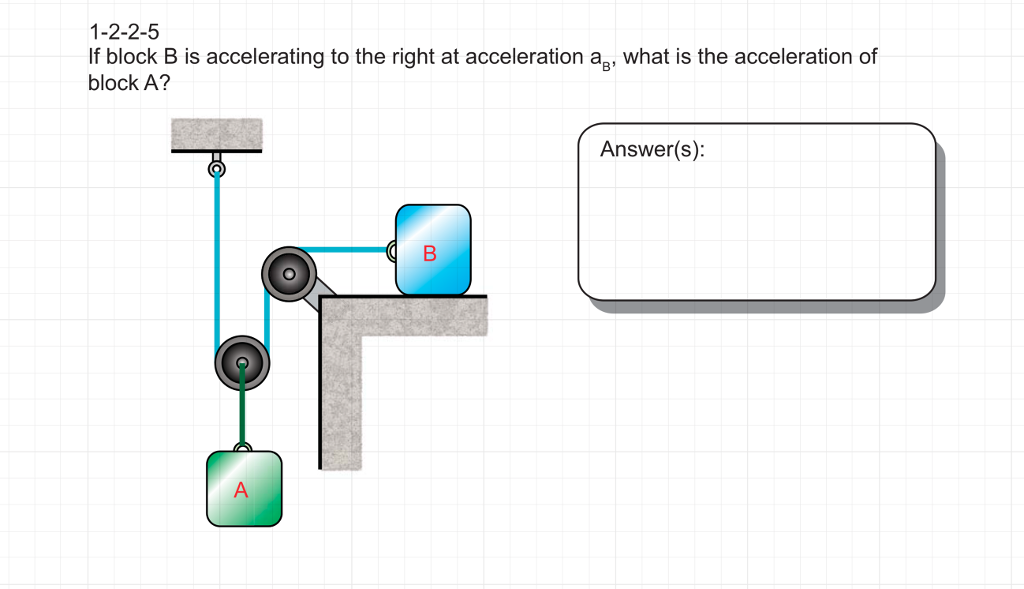
Solved 1 2 2 5 If Block B Is Accelerating To The Right At Chegg Here in the above figure we have a force that is applied vertically and horizontally. now apply newton's second law on the body and determine its acceleration. now let us consider the vertical motions acting on the body of mass 5 k g. Find the acceleration of the blocks a and b in the three situations shown in figure (5 e17). The system at rest, determine the acceleration of all the loads immediately after the lower thread keeping the system in equilibrium has been cut. assume that the threads are weightless, the mass of the pulley is negligible small, and there is no friction at the point of suspension. Explanation: to solve for the accelerations of blocks a and b in the given scenarios, we need to apply newton's second law to each block and consider the forces acting on them. we will also need to account for the tension in the string and the gravitational force.

Solved C Calculate The Acceleration Of The Block D After Chegg The system at rest, determine the acceleration of all the loads immediately after the lower thread keeping the system in equilibrium has been cut. assume that the threads are weightless, the mass of the pulley is negligible small, and there is no friction at the point of suspension. Explanation: to solve for the accelerations of blocks a and b in the given scenarios, we need to apply newton's second law to each block and consider the forces acting on them. we will also need to account for the tension in the string and the gravitational force. Knowing that the coefficient of static friction between the bundle of shingles and the horizontal platform is 0.30, determine the largest allowable acceleration a1 and the largest allowable deceleration a2 if the bundle is not to slide on the platform. In order to calculate the acceleration of the block in two cases (a and b), we first need to determine the friction force acting on the block. friction force can be calculated using the formula: friction force = coefficient of kinetic friction × normal force. Problem 2: consider the two systems (a) and (b) shown in the figure. for each system, determine the acceleration of block a. also, calculate the tension in the cable for the two block system. explain why the accelerations of block a are different for the two cases (1 point). 40 lb 40 lbs Α. p= 20 lb b 20 lb 30° 300 (a) (b). Friction between wall and block will be applied maximum equal to 1n but maximum friction available between block a and b is 10 n but if this will be there then relative motion will increase while friction is to oppose relative motion.

Solved C Calculate The Acceleration Of The Block D After Chegg Knowing that the coefficient of static friction between the bundle of shingles and the horizontal platform is 0.30, determine the largest allowable acceleration a1 and the largest allowable deceleration a2 if the bundle is not to slide on the platform. In order to calculate the acceleration of the block in two cases (a and b), we first need to determine the friction force acting on the block. friction force can be calculated using the formula: friction force = coefficient of kinetic friction × normal force. Problem 2: consider the two systems (a) and (b) shown in the figure. for each system, determine the acceleration of block a. also, calculate the tension in the cable for the two block system. explain why the accelerations of block a are different for the two cases (1 point). 40 lb 40 lbs Α. p= 20 lb b 20 lb 30° 300 (a) (b). Friction between wall and block will be applied maximum equal to 1n but maximum friction available between block a and b is 10 n but if this will be there then relative motion will increase while friction is to oppose relative motion.
Comments are closed.