Block Stacking Problem Pdf Force Triangle

Block Stacking Problem Pdf Force Triangle The block stacking problem is the following puzzle: place identical rigid rectangular blocks in a stable stack on a table edge in such a way as to maximize the overhang. To answer this question, three cases of increasing complexity are considered: single wide stacks, multiwide stacks that do not rely on friction, and multiwide stacks that do rely on friction.

Block Stacking Problem Pdf Mathematical Objects Mathematical Concepts We will now look at how building a stack of objects that are not aligned shifts their collective center of mass. figure(1) shows how the center of mass shifts as the blocks are placed on top of one another. The document contains various problems and solutions on the composition and resolution of forces using the parallelogram and triangle laws. it covers multiple cases with detailed examples and computations, including resultant forces and angles. B can push, but not pull, one another. thus, if block a rests on block b, then all the forces applied on block a by block b point upward, while all the forces applied on block b by block a point down. In the block stacking problem, a collection of blocks are to be stacked at a table edge. if we stack the blocks so that they protrude past the edge of the table, how far can they go horizontally?.
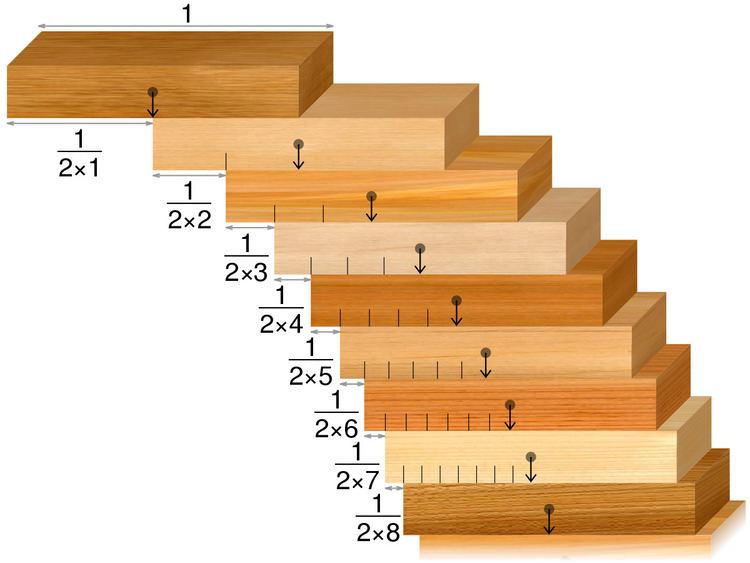
Block Stacking Problem Alchetron The Free Social Encyclopedia B can push, but not pull, one another. thus, if block a rests on block b, then all the forces applied on block a by block b point upward, while all the forces applied on block b by block a point down. In the block stacking problem, a collection of blocks are to be stacked at a table edge. if we stack the blocks so that they protrude past the edge of the table, how far can they go horizontally?. Here, we address this problem by designing an evolutionary algorithm; the proposed method is applied to two instances of the block stacking problem, maximizing the overhang for 20 and 50 block stacks. Tom block together with a stack of n − 1 blocks on top. in order to acheive the greatest possible offset with n blocks, the top n−1 blocks should themselves have the greatest possible offset, which is xn−1; otherwise, we could do better by replacing the top n − 1 bloc. We derive expressions for the joint probability density functions of block positions, and analyze their correlation. the study extends to the stochastic stability of a stack of given height, by exploring the statistical characteristics of the center of gravity of the part of tower above each block.
Comments are closed.