Binary Number Systems

Binary Number Systems Pdf Byte Computer Engineering The binary number system, also known as the base 2 system, uses only two digits, '0' and '1', to represent numbers. it forms the fundamental basis for how computers process and store data. A binary number is a number expressed in the base 2 numeral system or binary numeral system, a method for representing numbers that uses only two symbols for the natural numbers: typically "0" (zero) and "1" (one).
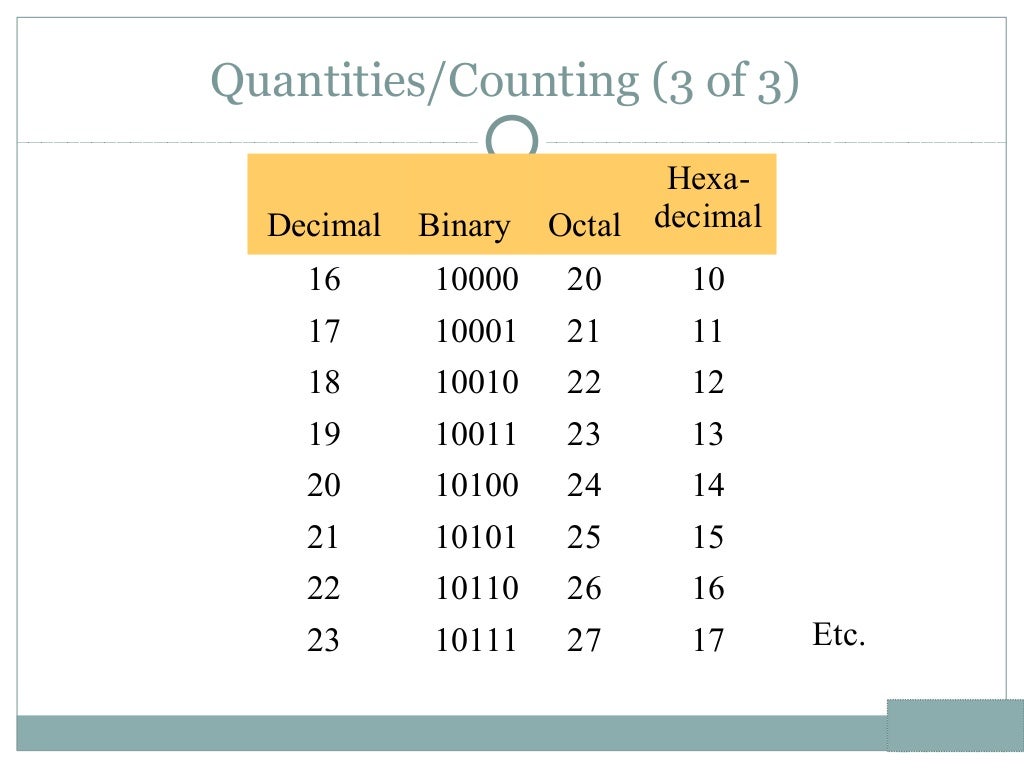
Binary Number Systems Learn how to count, convert and use binary numbers, which are made up of only 0s and 1s. see examples, diagrams, activities and words related to binary system. What is binary number system? the binary number system is a method of representing numbers that uses only two digits: 0 and 1. it is the foundation of all modern digital systems and computers. unlike the decimal system, which is based on ten digits (0 9), the binary system operates on base 2. Binary number system, in mathematics, positional numeral system employing 2 as the base and so requiring only two different symbols for its digits, 0 and 1, instead of the usual 10 different symbols needed in the decimal system. The article covers the basics of digital electronic circuits, explaining the binary number system, decimal to binary conversion, binary addition, voltage logic levels, and how bits, nibbles, and bytes relate to digital information processing.

The Basis Of Computing Binary Number Systems Explained Binary number system, in mathematics, positional numeral system employing 2 as the base and so requiring only two different symbols for its digits, 0 and 1, instead of the usual 10 different symbols needed in the decimal system. The article covers the basics of digital electronic circuits, explaining the binary number system, decimal to binary conversion, binary addition, voltage logic levels, and how bits, nibbles, and bytes relate to digital information processing. In our beginners introduction to binary, hexadecimal and octal numbers you will learn binary conversions and arithmetic with interactive demonstrations and detailed explanations. this binary tutorial is divided into 3 sections. The binary number system is of special importance in digital electronics, where only two values are possible: the “1” or “high” voltage level and the “0” or “low” voltage level. Data in digital circuits and computers is stored and transmitted as a series of zeros and ones and so various numbering systems are used to represent the data. conveniently, binary numbers have only two digits that are 0 and 1, so every piece of data (number) can be represented using a binary numbering system. Q: why do computer programmers confuse christmas and halloween? why? adjective: being in a state of one of two mutually exclusive conditions such as on or off, true or false, molten or frozen, presence or absence of a signal. from late latin bīnārius (“consisting of two”). terminology why? 10. 11. 100. 101. 110. 111. 1000. 1001. 1010. 1011. 1100.

Binary Number System Mathematical Mysteries In our beginners introduction to binary, hexadecimal and octal numbers you will learn binary conversions and arithmetic with interactive demonstrations and detailed explanations. this binary tutorial is divided into 3 sections. The binary number system is of special importance in digital electronics, where only two values are possible: the “1” or “high” voltage level and the “0” or “low” voltage level. Data in digital circuits and computers is stored and transmitted as a series of zeros and ones and so various numbering systems are used to represent the data. conveniently, binary numbers have only two digits that are 0 and 1, so every piece of data (number) can be represented using a binary numbering system. Q: why do computer programmers confuse christmas and halloween? why? adjective: being in a state of one of two mutually exclusive conditions such as on or off, true or false, molten or frozen, presence or absence of a signal. from late latin bīnārius (“consisting of two”). terminology why? 10. 11. 100. 101. 110. 111. 1000. 1001. 1010. 1011. 1100.

Binary Number System Washington Preparatory School Data in digital circuits and computers is stored and transmitted as a series of zeros and ones and so various numbering systems are used to represent the data. conveniently, binary numbers have only two digits that are 0 and 1, so every piece of data (number) can be represented using a binary numbering system. Q: why do computer programmers confuse christmas and halloween? why? adjective: being in a state of one of two mutually exclusive conditions such as on or off, true or false, molten or frozen, presence or absence of a signal. from late latin bīnārius (“consisting of two”). terminology why? 10. 11. 100. 101. 110. 111. 1000. 1001. 1010. 1011. 1100.
Comments are closed.