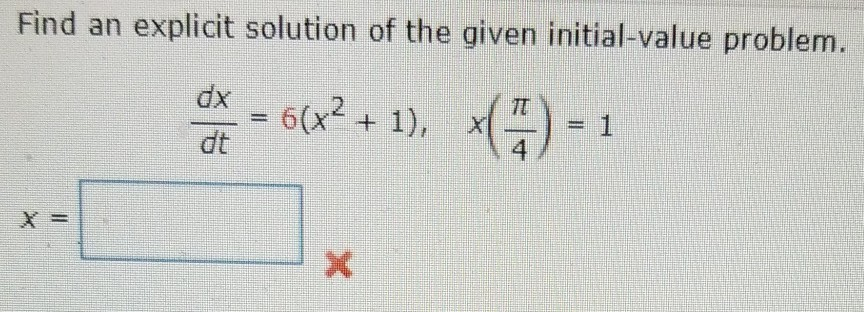
Solved Find An Explicit Solution Of The Given Initial Value Chegg Our expert help has broken down your problem into an easy to learn solution you can count on. there are 3 steps to solve this one. not the question you’re looking for? post any question and get expert help quickly. The explicit solution for the initial value problem is |y| = e^ ( (x^2 2) 2x ln (2)), with the interval of definition being ∞ < x < ∞. the constant of integration c is determined using the initial condition y (1) = 2, leading to c = ln (2).
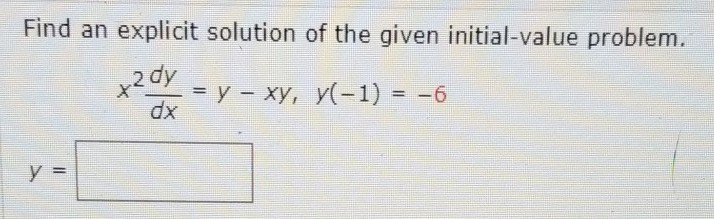
Solved Find An Explicit Solution Of The Given Initial Value Chegg An explicit form of the solution would be finding an expression for $y$ as a function of the independent variable. in this case this would be $x$ and not $t$ as stated in your question. An explicit solution of a differential equation expresses the dependent variable, usually y, directly in terms of the independent variable x. this is different from an implicit solution, where y and x might be intertwined in ways that make it challenging to solve for y. In this exercise we have to find the explicit solution for the given initial value problem. Your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. see answer question: find the solution of the given initial value problem in explicit form.
Answered Find An Explicit Solution Of The Given Initial Value Problem In this exercise we have to find the explicit solution for the given initial value problem. Your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. see answer question: find the solution of the given initial value problem in explicit form. An initial value problem (ivp) is a mathematical problem in which we seek to find a solution to a differential equation, subject to a specified initial condition. To find an explicit solution for the given** initial value problem**: 1 − y2dx − (1− x2)dy = 0 with the initial condition y (0) = 1 2, we can separate variables and integrate both sides of the equation: 1 − y2dx − (1− x2)dy = 0 rearrange it as: 1 − y2dx = (1 − x2)dy now, divide both sides by (1− y2) and multiply by dx on the. You'll get a detailed solution from a subject matter expert that helps you learn core concepts. find an explicit solution of the given initial value problem. we move all terms involving y to the left and all terms involving x to the right. this gives us: d y y 2 − 1 = d x x 2 − 1 show more…. Your solution’s ready to go! our expert help has broken down your problem into an easy to learn solution you can count on. see answer.
Comments are closed.