Analysis Ii Lecture 12 Part 1 The Tangent Space

Lecture 3 Curves In Space And Their Tangent Pdf Force Acceleration The tangent space of euclidean space (or of an open set in euclidean space) at a point is a vector space of the same dimension as that euclidean space. one can use a chart to define the. If we move with velocity ⃗v through space, then d⃗vt tells us at which rate the temperature changes for us. if we move with velocity ⃗v on a hilly surface of height h(x, y), then d⃗vh(x, y) gives us the slope we drive on.

Analysis Ii Ms Sol 2014 15 Pdf Space Mathematical Analysis The lecture notes were taken by a student in the class. for all of the lecture notes, including a table of contents, download the following file (pdf 1.6 mb). the lecture notes section includes the lecture notes files. De nition the vector space of smooth functions c1(m) on a smooth manifold m consists of all smooth functions f : m ! r. for u m open, the set c1(u) := ff : u ! r smoothg is also a vector space. elements of c1(u) are called local smooth functions (w.r.t. u). This can be shown analogously as completeness of `1(m), which was discussed in analysis 1 and will be addressed in the next lecture. the validity of the parallelogram law can deduced from its validity in the nite dimensional hilbert space rjm0j. 21. derivations at a point. we refer to theorem 1.40 in the script and the explanation that proceeds it.
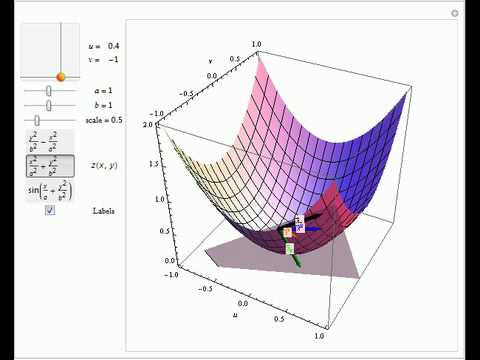
Tangent Space This can be shown analogously as completeness of `1(m), which was discussed in analysis 1 and will be addressed in the next lecture. the validity of the parallelogram law can deduced from its validity in the nite dimensional hilbert space rjm0j. 21. derivations at a point. we refer to theorem 1.40 in the script and the explanation that proceeds it. At every point of a smooth manifold mm there is a tangent space, an m dimensional vector space. the tan gent space is the space of derivations on c¥p (m), the algebra of germs of smooth functions. The tangent line (or simply tangent) to a curve at a given point is the straight line that touches the curve only at that point locally, and if you perturb it a little but fix this point, it will then touch the curve at more point(s) than this one. Contents how to study for analysis ii polya’s algorithm for solving problems list of symbols list of (named) theorems. In other words, an affine space has a constant tangent space. (by contrast, a curved space—smooth manifold—can have a variable tangent space; see remark 2.16.).

Tangent Space Visualization Math Reu At every point of a smooth manifold mm there is a tangent space, an m dimensional vector space. the tan gent space is the space of derivations on c¥p (m), the algebra of germs of smooth functions. The tangent line (or simply tangent) to a curve at a given point is the straight line that touches the curve only at that point locally, and if you perturb it a little but fix this point, it will then touch the curve at more point(s) than this one. Contents how to study for analysis ii polya’s algorithm for solving problems list of symbols list of (named) theorems. In other words, an affine space has a constant tangent space. (by contrast, a curved space—smooth manifold—can have a variable tangent space; see remark 2.16.).
Comments are closed.