An Approximate Comparison Of Ai Image Upscalers Enlargers R Photography

An Approximate Comparison Of Ai Image Upscalers Enlargers R Photography In mathematical notation, what are the usage differences between the various approximately equal signs "≈", "≃", and "≅"? the unicode standard lists all of them inside the mathematical operators b. And he could approximate small values by performing some mental math to get an accurate approximation to three decimal places. for example, approximating $e^ {3.3}$, we have$$e^ {3.3}=e^ {2.3 1}\approx 10e\approx 27.18281\ldots$$but what i am confused is how feynman knew how to correct for the small errors in his approximation.

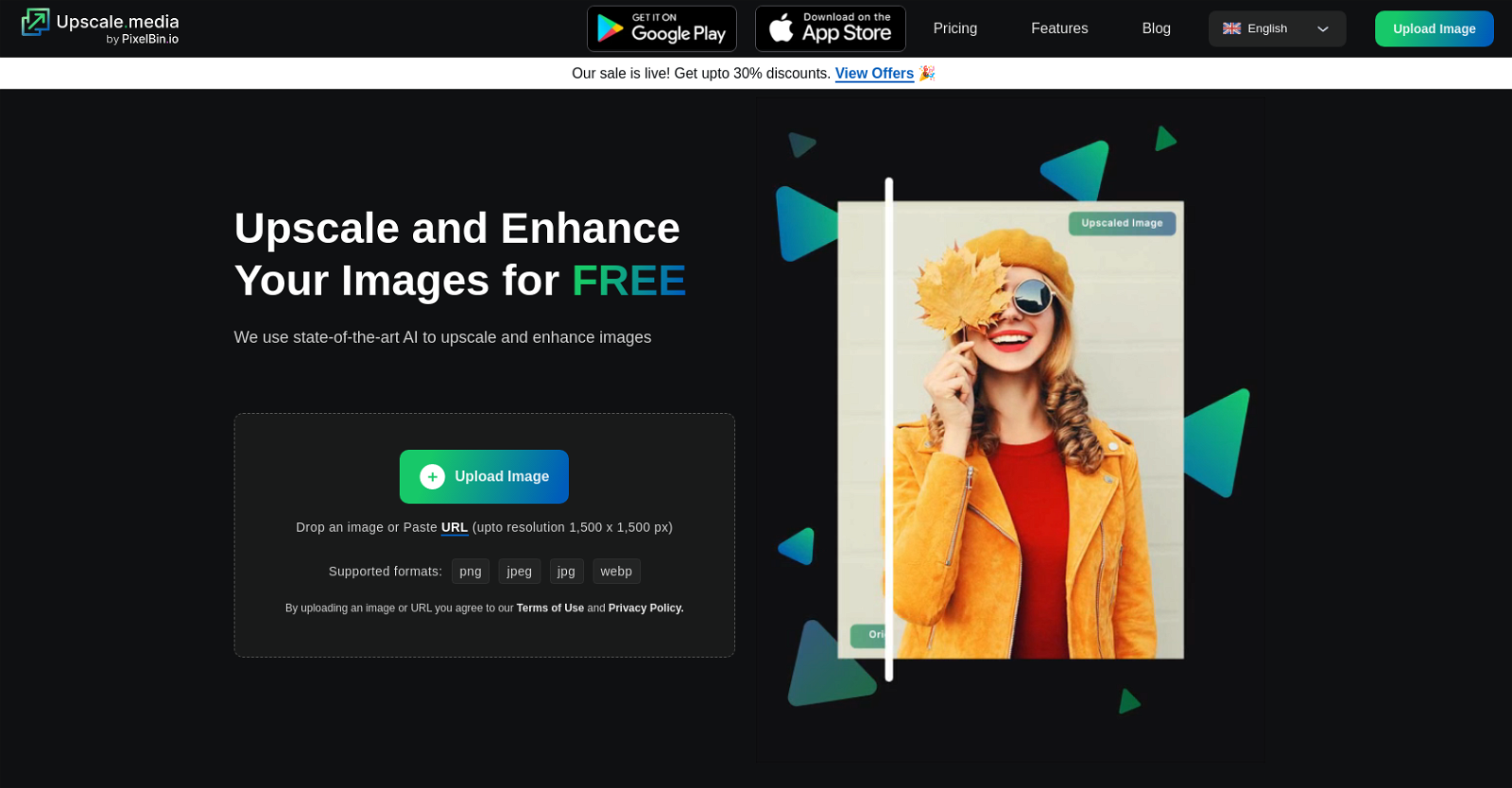
Ai Image Upscaler Vs Pictorial Comparison Ai Tools Images And Photos To indicate approximate equality, one can use ≃, ≅, ~, ♎, or ≒. i need to indicate an approximate inequality. specifically, i know a is greater than a quantity of approximately b. is there a way to. One can, for example, approximate continuous functions with polynomial functions, in which case the idea is to keep the area between the original function and the approximating function small. one can also specify the degree of approximation allowed. for example, we may want to restrict the area in the above example to a certain value. An approximate identity (in the sense that you've described) is a sequence of operators, usually derived from some "nice" class, that converge to the identity operator in the sense that you described. Approximate functional equation for the riemann zeta function ask question asked 6 years, 8 months ago modified 6 years, 8 months ago.

Image Upscale Ai Powered Enhancement For Stunning Visuals An approximate identity (in the sense that you've described) is a sequence of operators, usually derived from some "nice" class, that converge to the identity operator in the sense that you described. Approximate functional equation for the riemann zeta function ask question asked 6 years, 8 months ago modified 6 years, 8 months ago. Approximate piecewise constant function with continuous function ask question asked 4 years, 11 months ago modified 1 year, 3 months ago. We want to (manually) approximate $\sqrt {2}$ by using the first few terms of the binomial series expansion of \begin {align*} \sqrt {1 2x}&= \sum {n=0}^\infty \binom {\frac {1} {2}} {n} ( 2x)^n\qquad\qquad\qquad\qquad |x|<\frac {1} {2}\\ &= 1 x \frac {1} {2}x^2 \frac {1} {2}x^3 \cdots\tag {1} \end {align*} here we look for a way to determine. From this it follows that you can approximate from outside by open sets. in a bounded set, we may take complements without worry about infinite measure cropping up, so we can use the same logic to show that we can approximate from inside by closed sets. In fairness, both the title and the statement 'i am wondering what is the best way to approximate |x| with something smooth?' suggest a little more than an attempt to compute the derivative.

High Ai Picture Upscalers And Enlargers In 2023 Blog Approximate piecewise constant function with continuous function ask question asked 4 years, 11 months ago modified 1 year, 3 months ago. We want to (manually) approximate $\sqrt {2}$ by using the first few terms of the binomial series expansion of \begin {align*} \sqrt {1 2x}&= \sum {n=0}^\infty \binom {\frac {1} {2}} {n} ( 2x)^n\qquad\qquad\qquad\qquad |x|<\frac {1} {2}\\ &= 1 x \frac {1} {2}x^2 \frac {1} {2}x^3 \cdots\tag {1} \end {align*} here we look for a way to determine. From this it follows that you can approximate from outside by open sets. in a bounded set, we may take complements without worry about infinite measure cropping up, so we can use the same logic to show that we can approximate from inside by closed sets. In fairness, both the title and the statement 'i am wondering what is the best way to approximate |x| with something smooth?' suggest a little more than an attempt to compute the derivative.

Best Ai Upscaler For Photography 2025 Tested And Compared From this it follows that you can approximate from outside by open sets. in a bounded set, we may take complements without worry about infinite measure cropping up, so we can use the same logic to show that we can approximate from inside by closed sets. In fairness, both the title and the statement 'i am wondering what is the best way to approximate |x| with something smooth?' suggest a little more than an attempt to compute the derivative.