A Block Sliding On A Horizontal Frictionless Surface Is Attached To A Horizontal Spring With A Sprin

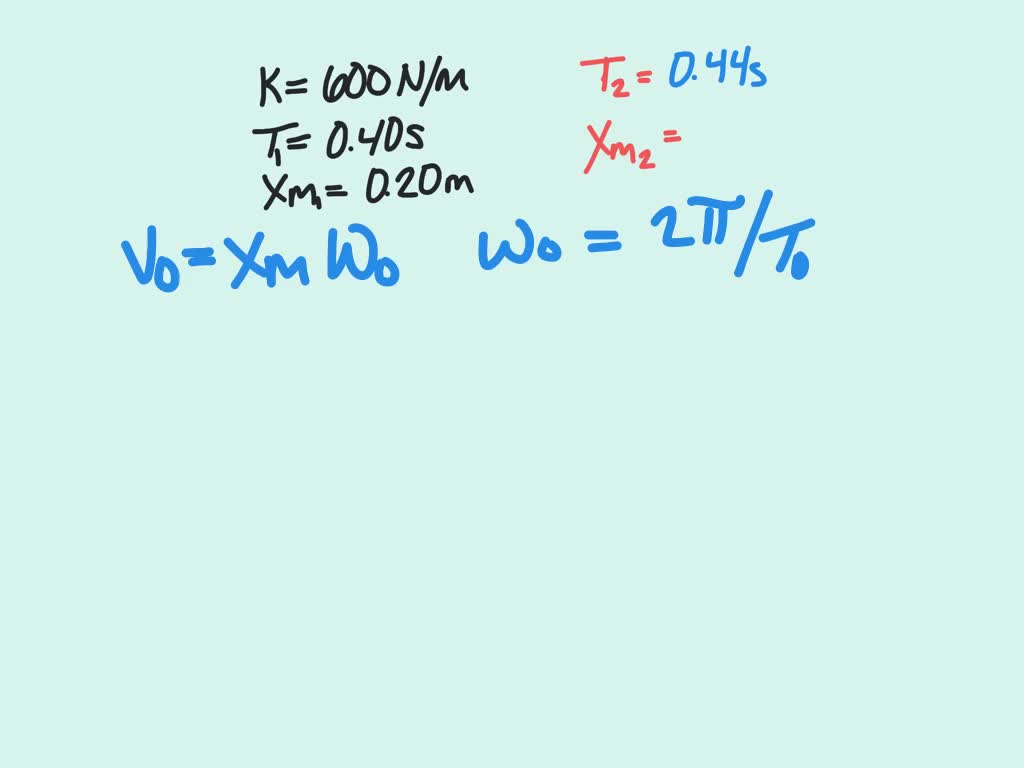
Solved A Block Sliding On A Horizontal Frictionless Surface Is Attached If the putty wad sticks to the block, determine (a) the new period of the motion and (b) the new amplitude of the motion. A block sliding on a horizontal frictionless surface is attached to a horizontal spring with a spring constant of 600 n m. the block executes shm about its equilibrium position with a period of 0.40 s and an amplitude of 0.20 m.

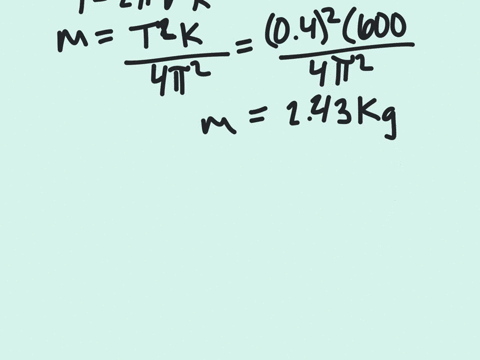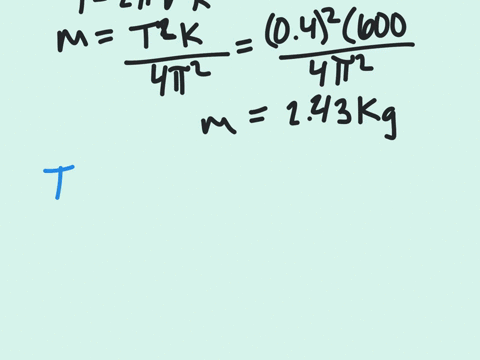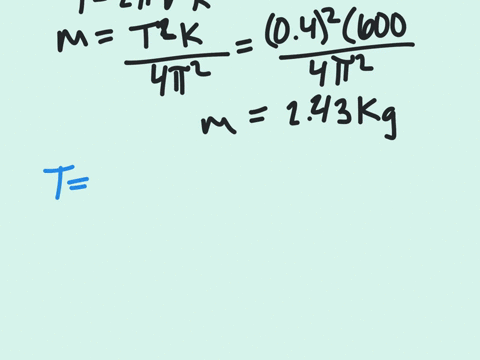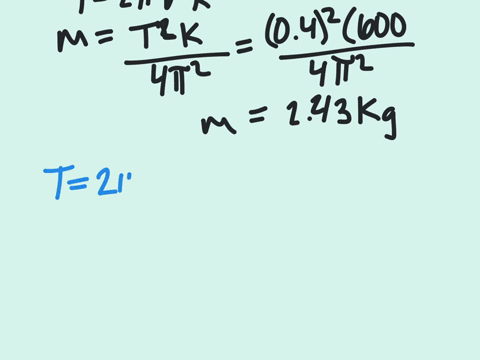
Solved A Block Sliding On A Horizontal Frictionless Surface Is Attached Understand the problem we have a block moving in simple harmonic motion (shm) due to a spring. a mass of putty is added when the block is at equilibrium, altering the system's mass and requiring us to find the new period and amplitude of motion. A 2.0 kg block is attached to one end of a spring with a spring constant of 100 n m and a 4.0 kg block is attached to the other end. the blocks are placed on a horizontal frictionless surface and set into motion. Our expert help has broken down your problem into an easy to learn solution you can count on. question: a block (mass = 4.0 kg) sliding on a horizontal frictionless surface is attached to one end of a horizontal spring (k = 100 n m) which has its other end fixed. A block sliding on a horizontal frictionless surface is attached to a horizontal spring with a spring constant of 600 ~n m. the block executes shm about its equilibrium position with a period of 0.40 seconds and an amplitude of 0.20 meters.

Solved A 1 5 Kg Block Sliding On A Horizontal Frictionless Chegg Our expert help has broken down your problem into an easy to learn solution you can count on. question: a block (mass = 4.0 kg) sliding on a horizontal frictionless surface is attached to one end of a horizontal spring (k = 100 n m) which has its other end fixed. A block sliding on a horizontal frictionless surface is attached to a horizontal spring with a spring constant of 600 ~n m. the block executes shm about its equilibrium position with a period of 0.40 seconds and an amplitude of 0.20 meters. The initial mechanical energy is given by the potential energy stored in the spring when the block is at its maximum displacement (amplitude): e initial = (1 2)ka^2 where a is the initial amplitude. A 0.30 kg ladle sliding on a horizontal frictionless surface is attached to one end of a horizontal spring (k = 500 n m) whose other end is fixed. the ladle has a kinetic energy of 10j as it passes. As the block slides through its equilibrium position, a 0.50 kg putty wad is dropped vertically onto the block. if the putty wad sticks to the block, determine (a) the new period of the motion and (b) the new amplitude of the motion. We can find the frequency of the block’s motion from angular frequency. then we can find the amplitude of the block’s motion using the formula for the maximum velocity of shm.